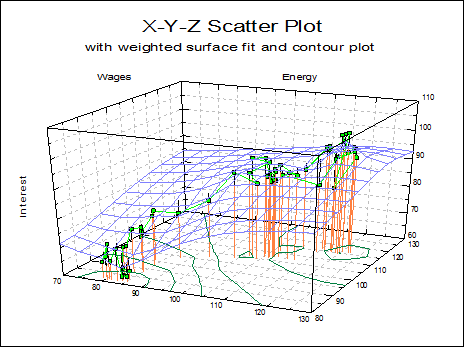
4.2.1. X-Y-Z Scatter Plot
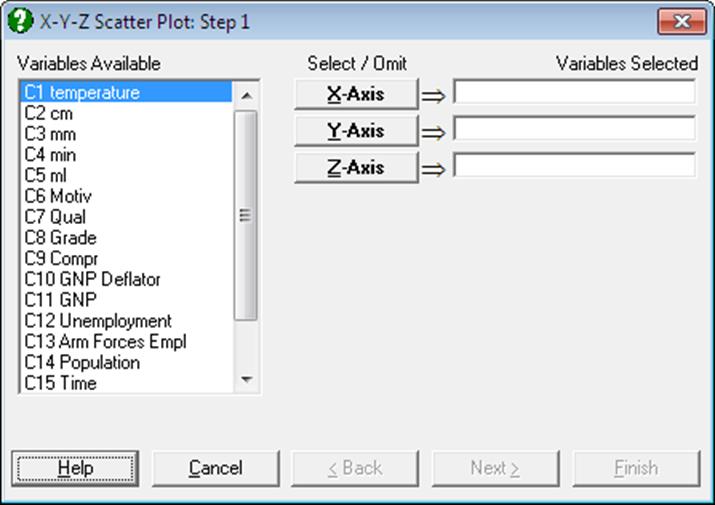
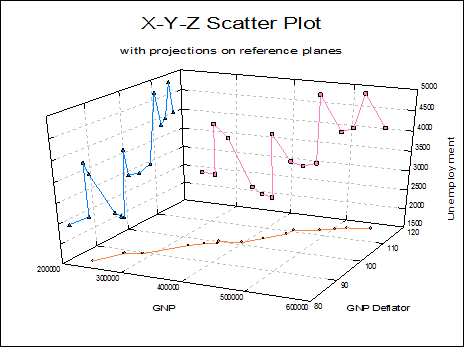
Three columns are selected by clicking on [X axis], [Y axis] and [Z axis]. Each axis can have the Scale Type Log base 10, Log base e, log based to any user-defined value, reciprocal, logit, probit, gompit (cloglog) or loglog. It is also possible to draw bivariate projection plots on X-Y, X-Z and Y-Z planes, error bars in any direction, fit linear regression planes and polynomial surfaces. Contours can be drawn for fitted surfaces.
Interactive Data Points: When the graph is still in Graphics Editor (i.e. before it is sent to Excel or Word), the data points plotted by this procedure are linked with the data in data matrix (see 2.3.2.3. Interactive Data Points). Move the mouse pointer over a data point and press down the right mouse button. A tooltip-like information panel will be displayed about that point until you release the right mouse button. If you are running UNISTAT in Stand-Alone Mode, the row of Data Processor containing this point will also be highlighted. If the delete key is pressed while highlighting a point, this point will be excluded from the plot and the graph will be redrawn. In Stand-Alone Mode, it is also possible to select a row of the spreadsheet to highlight the points on the graph which belong to this row.
Missing Values: Any point with at least one missing value is treated as missing.
Unequal Column Lengths: Columns with different lengths can be selected for X, Y and Z axes. Any triplet with at least one no data value will be considered as missing.
The Edit options specific to this procedure are as follows:
4.2.1.1. Viewpoint
As in all 3D Plots, you can alter the viewpoint and perspective options for the unit cube (see 2.3.4.6. 3D Viewpoint and Perspective).
4.2.1.2. Contours
When a surface is fitted on the data, contour curves can also be drawn (see 2.3.4.7. Contours).
4.2.1.3. X-Y-Z Points
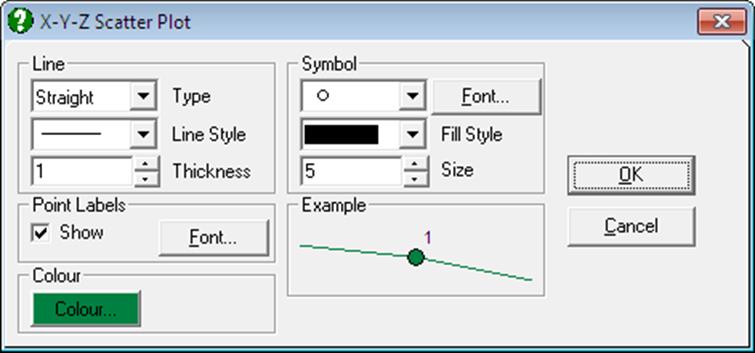
Line: If the Line Type option is set to Line, then the consecutive x-y-z points will be connected with straight lines. There is another Line field in the Planes dialogue, which is used for drawing bivariate projection plots on reference planes (see 4.2.1.4. Planes).
Symbol: Hundreds of different types of symbols can be selected for the x-y-z points (see 2.3.4.5.3. Symbols). Again, this is not to be confused with the Symbol field for the Planes dialogue.
Point Labels: Point Labels will be drawn alongside the x-y-z points. As in X-Y Plots, the text for Row Labels are used. If no Row Labels have been entered then the row numbers will be displayed.
4.2.1.4. Planes
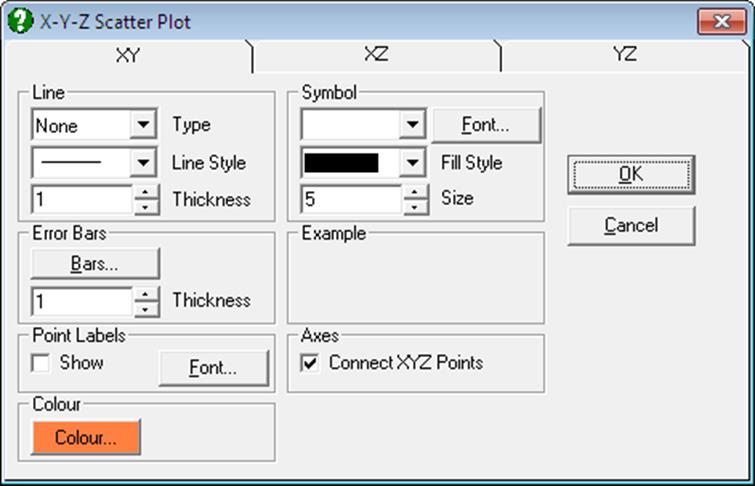
This dialogue controls how UNISTAT will draw bivariate plots on X-Y, X-Z and Y-Z planes, connect x-y-z points to reference Planes, and draw symmetric and asymmetric error bars on x-y-z points in any one of six directions.
Click on the desired tab to control the parameters for each plane.
Line: This frame is similar to the one in X-Y Plots (see 4.1.1.1.1. Line), except that the Curve and Frame options are not available for Line Type.
Symbol: Hundreds of different types of Symbols can be selected for the x-y points.
Point Labels: Point Labels will be drawn alongside the x-y points for the selected plane. As in X-Y Plots, the text for Row Labels are used. If no Row Labels have been entered then the row numbers will be displayed.
Connect X-Y-Z Points: If this box is checked, then each x-y-z point will be connected to the currently selected plane with a perpendicular line. On entry, this box will be checked for the X-Y plane.
Error Bars: This will control error bars in the direction perpendicular to the selected plane. For instance, when the Symmetric Bars option is selected for the X-Y Plane, then the up and down error bars will be drawn in the positive and negative Z directions.
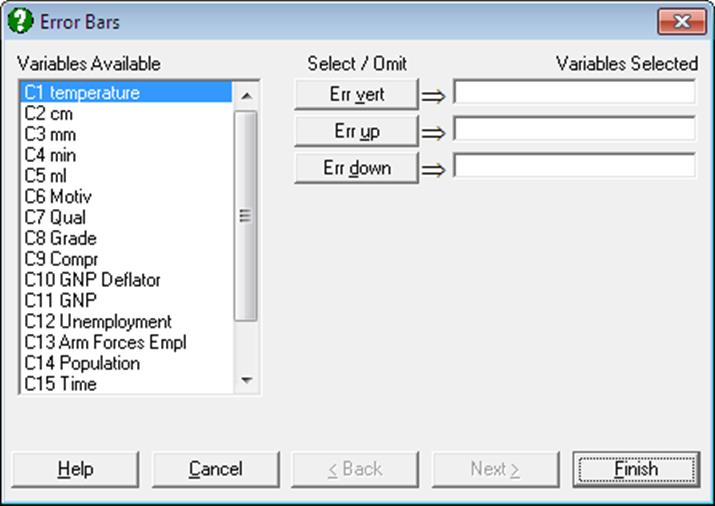
One or two data columns containing a dispersion measure (e.g. standard error, standard deviation) can be selected from the Variable Selection Dialogue. Error bars can be symmetric, in which case only one column is selected by clicking on [Err vert], or they can be asymmetric in which case the column containing up-pointing bars is selected by clicking on [Err up] and the one containing down-pointing bars is selected by clicking on [Err down]. Although the up and down options make sense for the Z direction, they must be interpreted as left and right or in and out for the X and Y directions.
In Stand-Alone Mode, columns containing means and standard errors for a range of data columns can be generated using the Range Statistics procedure in Data Processor. In Excel Add-In Mode, you can use one of Summary Statistics or Sample Statistics procedures with Output variables in rows option to create data for standard errors or standard deviations.
When calculating the minimum and maximum axis values the program will take error bars into consideration.
4.2.1.5. Surface Fitting
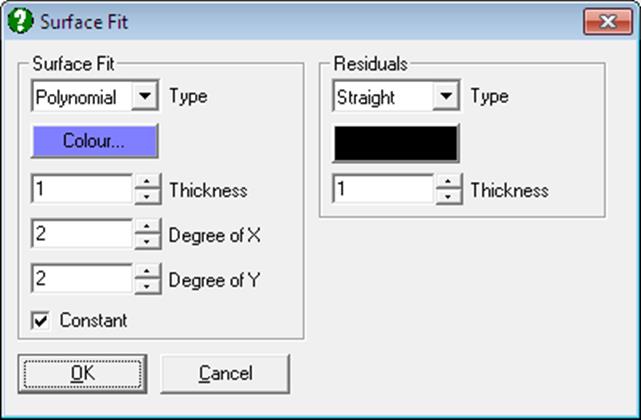
The Edit → Surface Fitting option provides access to three surface fitting options: Linear Regression Plane, Polynomial Surface and Weighted Averages Surface. In the first two cases you will have the option of fitting with or without a constant term.
Residual bars, i.e. the lines connecting each data point to the fitted surface can also be drawn. It is possible to control the colour and thickness of residual bars and whether they are to be displayed or not.
Coefficients of the fitted plane, as well as its R-squared and standard error values will be displayed in the legend object. However, since there may be up to 15 coefficients for the polynomial surface fit, they will not be displayed in the legend. In Stand-Alone Mode, it is also possible to run interpolations on the fitted curve, without having to retype these coefficients, using the Data Processor’s Reg function (see 3.4.2.6.3. UNISTAT Functions). The same coefficients will also be saved automatically in the file POLYCOEF.TXT, in the order of constant term (if any), X^1, X^2, …,Y^1, Y^2, …, Y^r for a degree r polynomial.
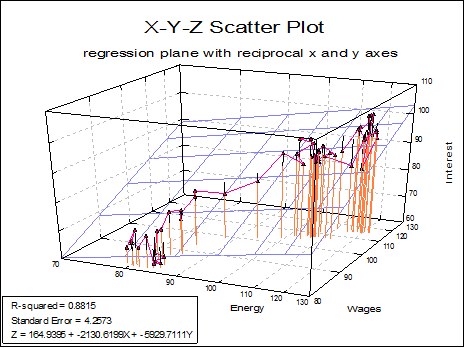
Linear Regression Plane: Output includes R-squared, standard error of regression and the equation of the plane fitted. When a log option is selected for an axis, the fitted values calculated using the Data Processor’s Reg function (see 3.4.2.6.3. UNISTAT Functions) must be transformed back to the original coordinates.
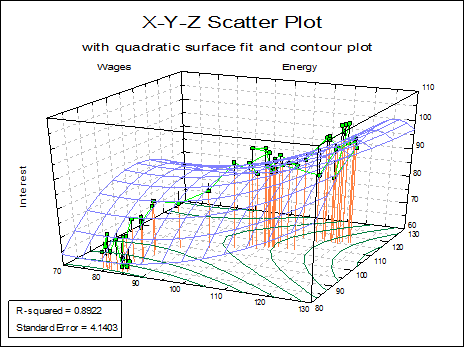
Polynomial Surface: The degree of X and Y variables can be determined independently and the constant term included or omitted. You must ensure that values of X and Y variables are not too large to cause a number overflow, particularly with higher degree polynomials.
Logarithmic and other nonlinear scaling options on X, Y and Z axes are available for polynomial surface fitting, but the contour curves will not be drawn. Coefficients of the fitted equation will be saved to the file POLYCOEF.TXT. It is also possible to run interpolations using the Data Processor’s Reg function (see 3.4.2.6.3. UNISTAT Functions).
Weighted Average: For each vertex of the mesh, the Z value of each point is weighted by the inverse square of its distance from the vertex, to form an average value for the fitted surface at this vertex.