9.1. Box-Jenkins ARIMA
9.1.0. Overview
ARIMA stands for Auto Regressive Integrated Moving Average model. So called, because the model fits autoregressive and moving average parameters to a transformed (differenced) time series and integrates back to the original scale before forecasts are generated. The differencing transformation makes use of B, the backshift operator, which shifts the subscript of a time series observation backwards in time by one period.
Select the column to analyse by clicking on [Dependent]. This column should not contain any missing values.
9.1.1. Differencing Input Options
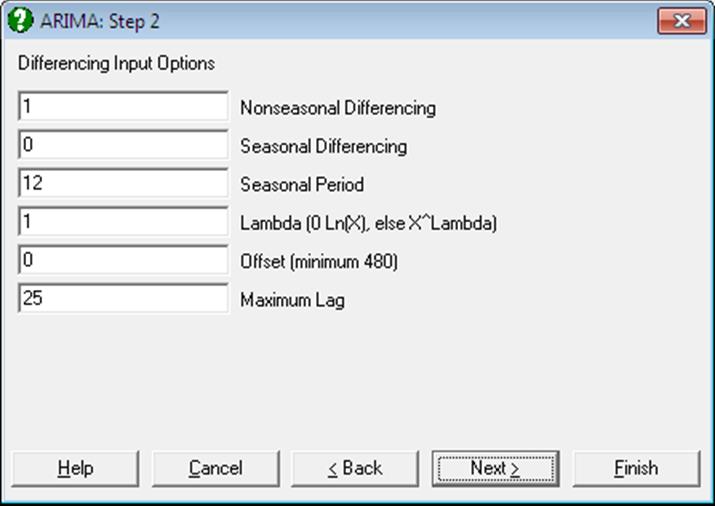
The Differencing Input Options dialogue is for entering the parameter values used in transforming the original data. The data can be transformed by differencing, taking logs, raising to a power and adding an offset to it.
Nonseasonal Differencing: The degree of differencing across whole series (d).
Seasonal Differencing: The degree of differencing between points with seasonal period units apart in the series (D).
Seasonal Period: The number of time units per season (s).
Lambda: This is a coded value which determines any logarithmic or power transformation. This is performed before any differencing:
= 1 No Effect 
= 0 Log of series 
else 
Offset: The value of offset is added to every value in the time series. This is used to allow taking logarithms of a series including negative values.
Maximum Lag: This is the maximum lag to calculate in correlation displays.
You can apply any transformation to the series during the data preparation phase. In this case, forecasts will be generated in the transformed scale. Transformations made within Box-Jenkins ARIMA are reversed to give forecasts in the original scale.
The program then displays a dialogue with two options. The Fit Model option proceeds with the next step in the analysis (where the Box-Jenkins ARIMA model is selected.) and the Differencing Output Options gives access to the intermediate results.
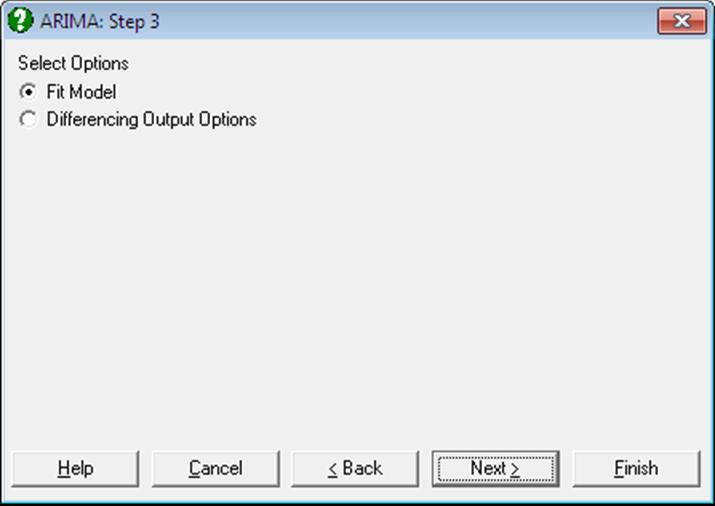
The Fit Model option should not be selected until the data series has been transformed into a stationary series.
9.1.2. Differencing Output Options
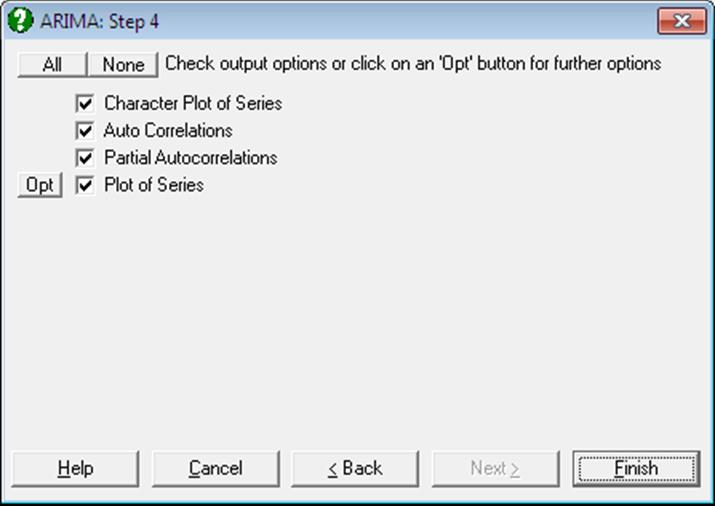
Differencing Output Options should be used to help set the transformation values before the model is estimated. You may move between this dialogue and the second dialogue a number of times before the series is transformed appropriately. The input series for the Box-Jenkins ARIMA model must be stationary. A stationary series has a constant mean, variance and autocorrelation. Also, the Autocorrelation Function and Partial Autocorrelation Function should give an idea about the number of parameters to fit to the model.
Character Plot of Series: The transformed series is displayed in the form of a character plot together with the values.
Autocorrelation Function: The Autocorrelation Function (ACF) displays the autocorrelations of the transformed series. The autocorrelation represents the correlation between points in the series at displacement lag. The number of autocorrelations displayed is controlled in the Differencing Input Options dialogue.
In Box-Jenkins ARIMA modelling the series is required to be stationary. If the ACF either cuts off fairly quickly or dies down fairly quickly, then the time series values should be considered stationary. If the ACF dies down extremely slowly, then the time series values should be considered non stationary and some differencing will be required.
The ACF should be examined to decide which model to fit in the final stages.
Partial Autocorrelation Function: The Partial Autocorrelation Function (PACF) displays the partial autocorrelations of the transformed series. The partial autocorrelations represent the correlation between points in the series at displacement lag, with the effects of the intervening observations eliminated. Hence the partial autocorrelation at lag 1 is equivalent to the autocorrelation at lag 1. The number of autocorrelations displayed is controlled in the Differencing Input Options dialogue.
The PACF should be examined to decide which model to fit in the final stages.
Hi-Res Plot of Series: This displays a graphical view of the transformed series.
Example
Table 3.1 on p. 83 from Bowerman, Bruce L. & Richard T. O’Connell (1987). Data on monthly Hotel Room Averages for 1973-1986 are given.
Open TIMESER, select Statistics 2 → Box-Jenkins ARIMA and Room Averages (C1) as [Variable]. At the Differencing Input Options dialogue enter:
· 0 Nonseasonal Differencing
· 1 Seasonal Differencing
· 12 Seasonal Period
· 0 Lambda (0 Log(X), else X^Lambda)
· 0 Offset (minimum 480)
· 25 Maximum Lag
Check all differencing output option boxes to obtain the following results:
ARIMA
Character Plot of Series: Room Averages
|
Row |
X(t) |
-0.0263 0.0831 |
|
1 |
0.0334 |
* |
|
2 |
0.0020 |
* |
|
3 |
0.0465 |
* |
|
4 |
0.0357 |
* |
|
5 |
0.0484 |
* |
|
… |
… |
… |
Autocorrelations: Room Averages
|
Lag |
Correlation |
Standard Error |
-1.0000 1.0000 |
|
1 |
0.1933 |
0.0801 |
( *****)* |
|
2 |
0.0244 |
0.0830 |
( ** ) |
|
3 |
-0.2442 |
0.0830 |
***(**** ) |
|
4 |
-0.1515 |
0.0875 |
(***** ) |
|
5 |
-0.2119 |
0.0892 |
*(***** ) |
|
… |
… |
… |
… |
Partial Autocorrelations: Room Averages
|
Lag |
Correlation |
Standard Error |
-1.0000 1.0000 |
|
1 |
0.1933 |
0.0801 |
( *****)* |
|
2 |
-0.0135 |
0.0801 |
( * ) |
|
3 |
-0.2560 |
0.0801 |
***(**** ) |
|
4 |
-0.0622 |
0.0801 |
( ** ) |
|
5 |
-0.1760 |
0.0801 |
*(**** ) |
|
… |
… |
… |
… |
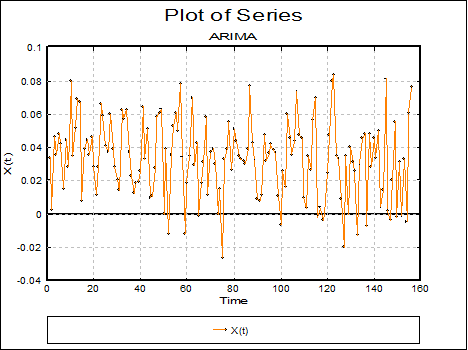
9.1.3. Model Fitting
The Model Fitting dialogue should only be used when the time series is considered stationary. The following guidelines can be used to help choose an Box-Jenkins ARIMA model to fit. It is often possible to try different models on the same data.
9.1.3.1. Seasonal and Nonseasonal Operators
Nonseasonal Operators (p and q)
The ACF has spikes at lags 1, 2, …, r and cuts off after lag r, and the PACF dies down; use q = r and p = 0.
The ACF dies down and the PACF has spikes at lags 1, 2, …, r and cuts off after lag r; use q = 0 and p = r.
The ACF has spikes at lags 1, 2, …,r and cuts off after lag r, and the PACF has spikes at lags 1, 2, … ,s and cuts off after lag s; use q = r and p = s.
The ACF contains small autocorrelations at all lags and the PACF contains small autocorrelations at all lags; use q = 0 and p = 0.
The ACF dies down and the PACF dies down; use p = 1 and q = 1.
Seasonal Operators (P and Q)
The previous guidelines apply to P and Q, but only consider autocorrelations at s, 2s, 3s, … where s is the seasonal period.
9.1.3.2. Model Fitting Parameters
The Model Fitting dialogue requires inputting the following parameters:
Overall Constant: If the overall constant value is non
zero, then 
is included in the model,
otherwise it is not.
Nonseasonal AR Parameters: The nonseasonal AR parameter determines the number of nonseasonal autoregressive parameters (p) to include in the model. This value is normally not larger than 2.
Nonseasonal MA Parameters: The nonseasonal MA parameter determines the number of nonseasonal moving average parameters (q) to include in the model. This value is normally not larger than 2.
Seasonal AR Parameters: The seasonal AR parameter determines the number of seasonal autoregressive parameters (P) to include in the model. This value is normally not larger than 2.
Seasonal MA Parameters: The seasonal MA parameter determines the number of seasonal moving average parameters (Q) to include in the model. This value is not normally larger than 2.
Backforecasts: This is the number of backforecasts generated before the model is fitted. If this value is zero then no backforecasts are generated.
Maximum Number of Iterations: The maximum number of iterations is the number of iterations allowed before the model declares non convergence.
The model fitted is given by the following equations:
where:
·
is the overall constant.
·
is the AR
operator.
·
is the MA operator.
·
is the seasonal AR
operator.
·
is the seasonal MA
operator.
·
is the seasonal white noise.
·
is the white noise and
assumed 
The model is fitted by an iterative least squares method. The output options are accessed by selecting the ARIMA Results from the following dialogue.
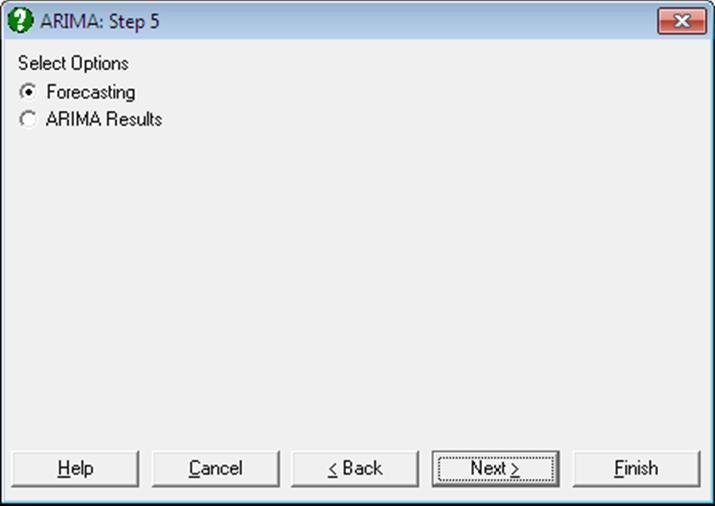
9.1.4. Model Output Options
When a model has been fitted, you will have the following output options:
Model Results: The number of iterations made and the transformation used are displayed. For each fitted parameter the estimated value, the standard error and the t-value are displayed.
Parameter Covariance Matrix: A table of the covariance between each fitted parameter is displayed.
Parameter Correlation Matrix: A table of the correlation between each fitted parameter is displayed.
Plot of Residuals: This displays the residual values in a table and allows them to be saved back to the data matrix.
Residual Autocorrelation: This displays the Autocorrelation Function of the residuals. The residuals should be unrelated because the model should account for the relationship in the time series data. If the residuals are unrelated then the autocorrelations of the residuals should be small. The Ljung-Box statistic (see below) is a test of the residual autocorrelations.
Ljung-Box Statistic: This displays the Ljung-Box statistic, the degrees of freedom and the associated chi-square probabilities at various values up to the lag. The Ljung-Box statistic is a test of the relationship between the residuals. A large value shows the residuals to be related, and hence the model being inadequate.
Example
Following the example in Differencing Output Options, select Fit Model to select an Box-Jenkins ARIMA model. On the Model Fitting dialogue enter:
· 1 Overall Constant (0 No, Else Yes)
· 3 Nonseasonal AR Parameters (P)
· 0 Nonseasonal MA Parameters (Q)
· 0 Seasonal AR Parameters (Ps)
· 1 Seasonal MA Parameters (Qs)
· 0 Backforecasts
· 200 Maximum Number of Iterations
· 0.0001 Tolerance
On the Model Output Options dialogue check only the Model Results box to obtain the following results:
ARIMA: Fit Model
Model Results
Transformation: X(t) = (1-B^12) log(Room Averages)
|
Parameter |
Estimate |
Std error |
t ratio |
|
Overall Constant |
0.02699 |
0.01690 |
1.5976 |
|
(AR) P(1) |
0.26089 |
0.06798 |
3.8380 |
|
(AR) P(2) |
0.15688 |
0.06293 |
2.4929 |
|
(AR) P(3) |
-0.23467 |
0.07074 |
-3.3175 |
|
(SMA) Qs(1) |
0.51389 |
0.07311 |
7.0293 |
|
Number of Iterations = |
148 (Converged) |
|
Seasonal Period = |
12 |
The numbers obtained here are not identical to the ones given in the book, though the general characteristics of the fitted models are similar. This is due to the highly iterative nature of the estimation process and the results may differ from one implementation to the other.
9.1.5. Forecasting
9.1.5.1. Forecasting Input Options
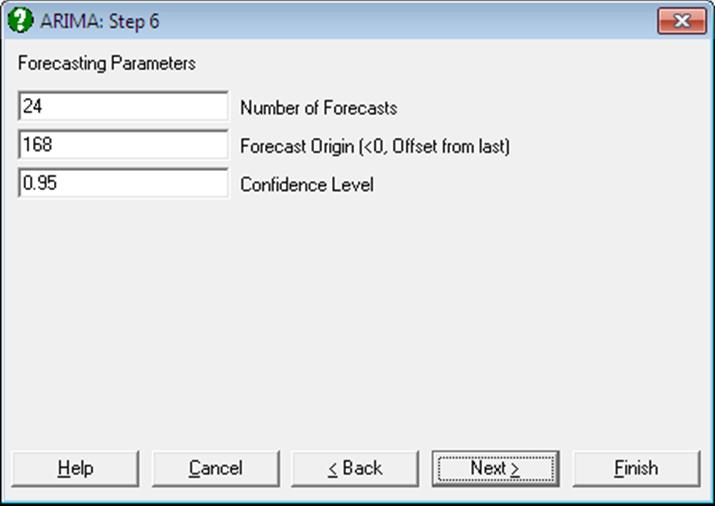
This dialogue requests the following parameters:
Number of Forecasts: This is the number of forecasts to be generated.
Forecast Origin (<0, Offset): The forecast origin determines the location in the series at which the forecasts will start. If you enter a positive value, this is used as the forecast origin. If 0 is entered, then the last point in the series is used as the origin. If a negative value is entered, then this value is used as an offset from the last point. For instance, -1 represents the penultimate point as the forecast origin.
Confidence Level: The forecasts will be given with confidence intervals at this level. The value must be greater than 0 and less than 1. Typical values are 0.95, 0.99 or 0.9.
9.1.5.2. Forecasting Output Options
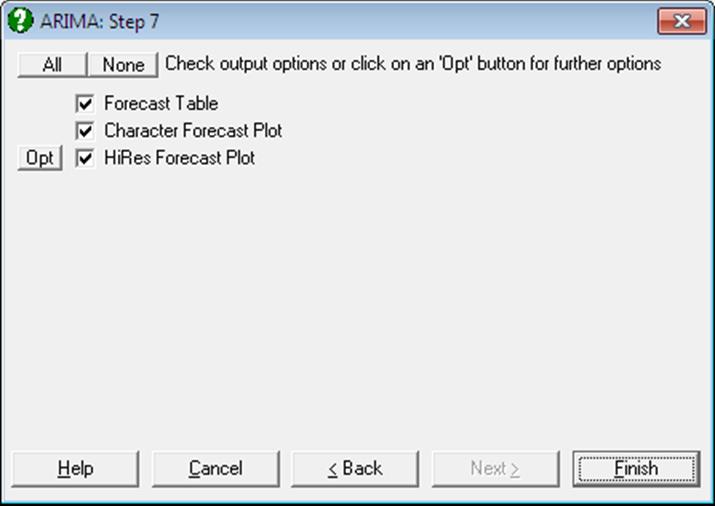
When the above parameters have been specified, the following output options will be available:
Forecast Table: A table of forecasts and confidence intervals from the given forecast origin is displayed.
Character Forecast Plot: A character plot of the original data, lead 1 forecasts and forecasts from the forecast origin are displayed.
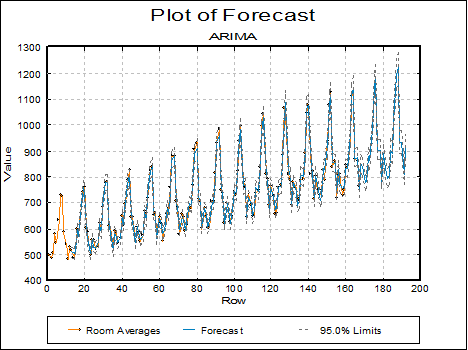
Plot of Forecast: A graphical display of the original data, lead 1 forecasts and forecasts from the forecast origin is generated. These are the same values as the Character Forecast Plot.
Example
Following the example in Model Output Options dialogue select Forecasting. On the Forecasting Input Options dialogue enter:
· 24 Number of Forecasts
· 168 Forecast Origin (<0, Offset from last)
· 0.95 Confidence Level
Select the Forecast Table output option to obtain the following results:
ARIMA: Forecasting
Forecast Table: Room Averages
Forecasts with Origin at 168
|
Row |
Forecast |
Lower 95% |
Upper 95% |
|
169 |
840.0521 |
808.0632 |
873.3075 |
|
170 |
771.1056 |
741.7421 |
801.6315 |
|
171 |
777.0039 |
747.4158 |
807.7633 |
|
172 |
872.1992 |
838.9860 |
906.7271 |
|
173 |
858.4281 |
825.7393 |
892.4109 |
|
174 |
982.0313 |
944.6357 |
1020.9071 |
|
175 |
1154.9294 |
1110.9500 |
1200.6498 |
|
176 |
1181.2955 |
1136.3121 |
1228.0598 |
|
177 |
902.9520 |
868.5678 |
938.6974 |
|
178 |
903.5714 |
869.1636 |
939.3412 |
|
179 |
783.1983 |
753.3743 |
814.2029 |
|
180 |
892.2127 |
858.2375 |
927.5330 |
|
181 |
860.6177 |
823.8597 |
899.0157 |
|
182 |
794.2411 |
760.3182 |
829.6776 |
|
183 |
804.2494 |
769.8990 |
840.1324 |
|
184 |
903.2180 |
864.6406 |
943.5167 |
|
185 |
888.6314 |
850.6769 |
928.2792 |
|
186 |
1015.3943 |
972.0257 |
1060.6980 |
|
187 |
1193.5981 |
1142.6182 |
1246.8526 |
|
188 |
1220.5764 |
1168.4441 |
1275.0345 |
|
189 |
933.1099 |
893.2557 |
974.7422 |
|
190 |
933.8563 |
893.9703 |
975.5220 |
|
191 |
809.5330 |
774.9569 |
845.6517 |
|
192 |
922.2238 |
882.8345 |
963.3704 |
