9.4.1. Life Table

The Life Table is useful in analysing data on failure times when some of the cases are censored. That is, when the time of failure is not known for them. First, the data is grouped into a number of intervals, spanning a time period specified by the user. Let:

·        d_j = number of deaths at interval j, and

·        c_j = number of censored cases at interval j.

·        n_j = number of cases entering interval j.

The average number of cases who are at risk at interval j is then defined as:

    

The Life Table estimates the survival function as:

    

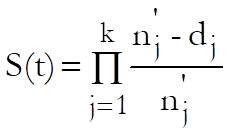
The survival and hazard functions are estimated and they are displayed together with their standard errors and confidence intervals for a user-defined confidence level (the default is 0.95).

9.4.1.1. Life Table Interval Selection

Once the time and optional status and factor variables have been selected (see 9.4.0. Survival Analysis Variable Selection), a second dialogue will ask for the intervals into which the data will be grouped.

UNISTAT will suggest a suitable selection that will cover the data in a regular pattern of intervals. It is also possible to enter a number of irregular intervals.

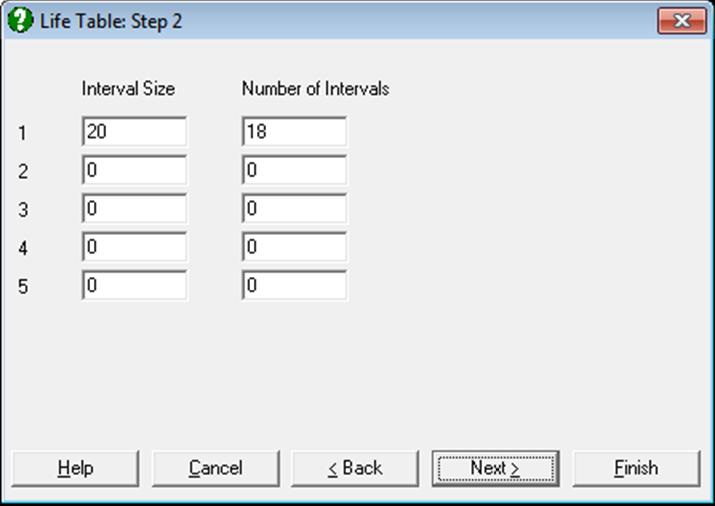
The interval selection dialogue presents a matrix of text fields with five rows and two columns. For a model with regular intervals (the most common practice) it is sufficient to fill in the first row of the matrix. The first column Interval Size is used to enter the duration of each interval and the second column No of Intervals is for entering the number of intervals of this size. Consider the following input:

 

Interval Size	No of Intervals
5	4
10	2
0	0
0	0
0	0

This would result in the following intervals.

 

Interval Start
0	4 intervals of size 5 time units
5
10
15
20	2 intervals of size 10 time units.
30

When the total time span covered by the table does not include the entire data set, only those cases within the table range will be included in the model. If, on the other hand, the specified intervals cover more than the maximum time in data, then the Life Table will not display intervals after the last termination or censoring date.

9.4.1.2. Life Table Output Options

selection stage, then the program displays a further dialogue allowing you to select levels for which output is to be generated.

Next, the model is estimated and an Output Options Dialogue is displayed.

9.4.1.2.1. Life Table

You can select to display one or more of the following columns of the Life Table.

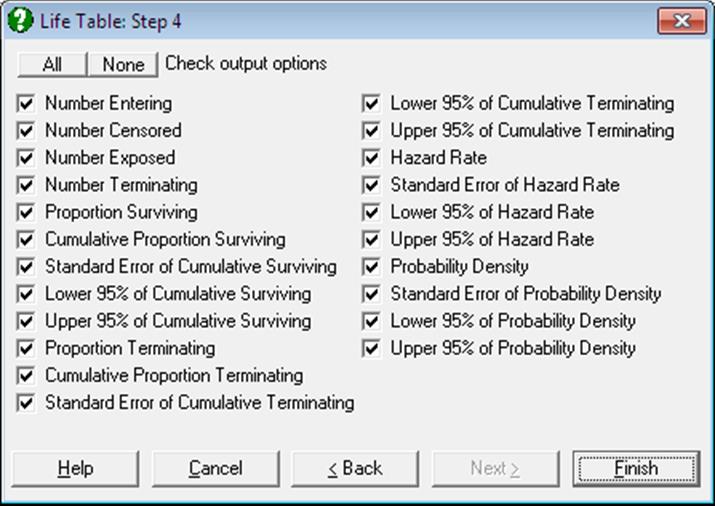
Although the table options could have been grouped under four main categories of (1) Survival Function, (2) Hazard Function, (3) Hazard Rate and (4) Probability Density (together with their standard errors and confidence intervals), here we prefer to combine them under one table to avoid repetitions. You can always obtain the desired table by unchecking the unwanted table columns.

Interval Start: The time at the start of the interval.

Number Entering:

n_j: The number of cases that enter the interval.

Number Censored:

c_j: The number of cases that are censored in the interval.

Number Exposed:

     

This can be considered as the number of cases that are at risk of the terminal event in the interval.

Number Terminating:

d_j: The number terminating is the number of cases that reach the terminal event within the interval.

Proportion Surviving:

     

The proportion surviving is the proportion of cases that do not reach the terminal event in this interval.

Cumulative Proportion Surviving:

     

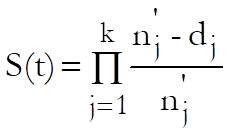
The cumulative proportion surviving is the proportion of cases that have not reached the terminal event by the end of the interval.

Standard Error of Cumulative Surviving:

     

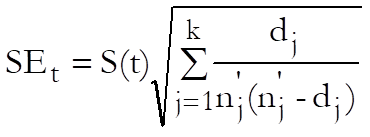
The standard error of cumulative proportion surviving is computed from Greenwood’s formula (Collett, 1994).

Confidence Intervals of Cumulative Surviving:

     

where the log-transformed standard error is:

     

SE_t (the standard error reported in the table) is not used in computing the confidence intervals, employing the standard Z distribution, because it often leads to values outside the valid range of 0 – 1. The significance level can be set to any value between 0 and 1 from the Variable Selection Dialogue.

Proportion Terminating:

     

The proportion of cases that reach the termination event in this interval, which is equal to one minus proportion surviving.

Cumulative Proportion Terminating:

1-S(t): This is the cumulative proportion of cases that have reached the terminal event by the end of the interval and it is equal to one minus cumulative proportion surviving.

Standard Error of Cumulative Terminating:

SE_t: This is identical to the standard error of cumulative proportion surviving.

Confidence Intervals of Cumulative Terminating:

     

This is equal to one minus confidence intervals of surviving.

Hazard Rate:

     

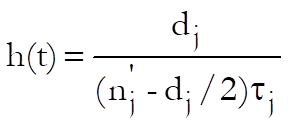
where  is the length of interval j.

The hazard rate is an estimate of the probability per unit time that cases entering the interval will experience the terminal event in the interval.

Standard Error of Hazard Rate:

     

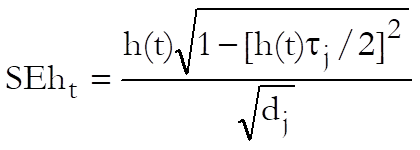
The asymptotic standard error of the hazard rate is displayed.

Confidence Intervals of Hazard Rate:

     

Confidence intervals are computed from the Z distribution.

Probability Density:

     

The probability density is an estimate of the probability per unit time of the terminal event occurring in the interval.

Standard Error of Probability Density:

     

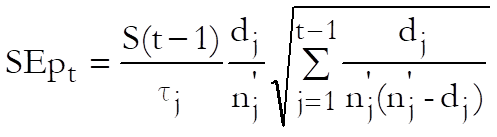
The standard error of the probability density is displayed.

Confidence Intervals of Probability Density:

     

Confidence intervals are computed from the Z distribution.

9.4.1.2.2. Life Table Plots

Four Life Table plots can be displayed. The Edit → Data Series dialogue provides you with necessary controls to edit all aspects of the plot. If a factor column was selected, each subgroup’s settings are controlled from a different tab on the same dialogue. There are no limitations on the maximum number of subgroups that can be plotted on one graph, but only the properties of the first nine subgroups can be controlled from the Edit → Data Series dialogue.

For the plot of survival and hazard functions, the line type is set to Step Right by default (see 4.1.1.1.1. Line), following Armitage & Berry (1994) and Altman (1991). But this can be changed to Step Down following Collett (1994), or any other type from the Edit → Data Series → Line dialogue.

It is possible to display standard errors or confidence intervals for each subgroup separately. To do this, first display the graph and then select Edit → Data Series. Clicking on the [Bars…] button, a small dialogue will pop up.

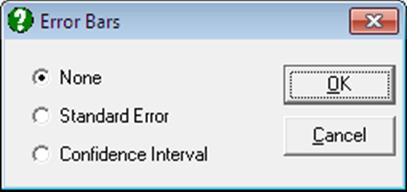
If the second option Standard Error is selected, then symmetric error bars are drawn for each point of the particular series selected. If the third option Confidence Interval is selected, then asymmetric error bars are drawn for confidence intervals displayed in Life Table.

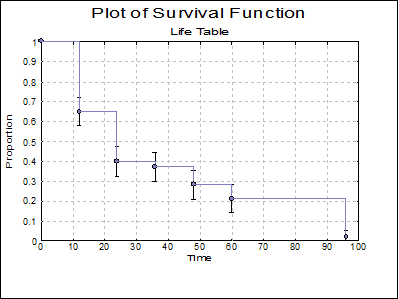
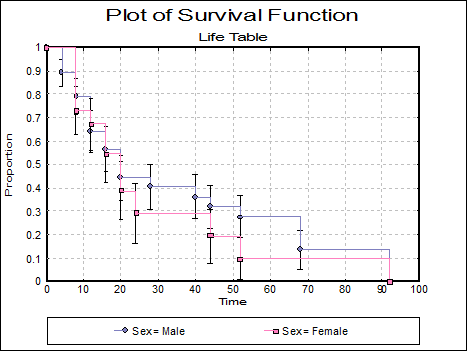
Plot of Survival Function: A plot of the cumulative proportion surviving is displayed.

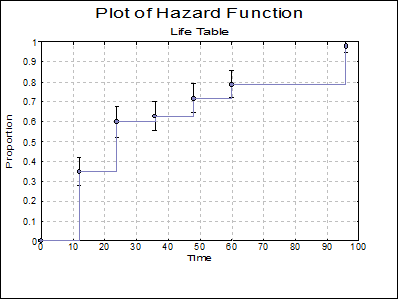
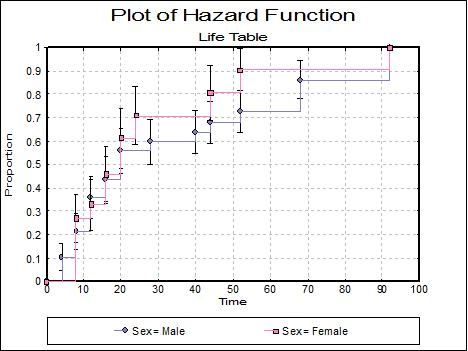
Plot of Hazard Function: A plot of the cumulative proportion terminating is displayed.

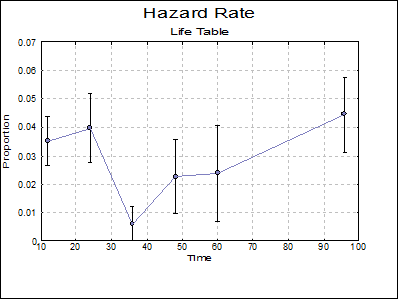
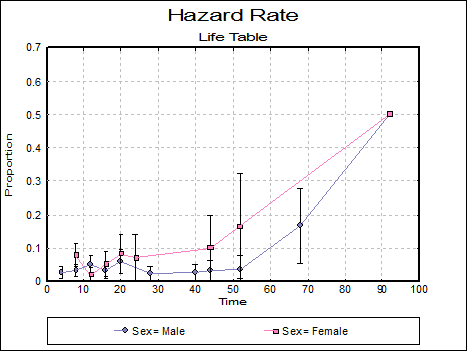
Plot of Hazard Rate: A plot of the hazard rate is displayed for each factor level. Select Error Bars in the Edit → Data Series dialogue to display standard errors or confidence intervals of the probability density function as error bars.

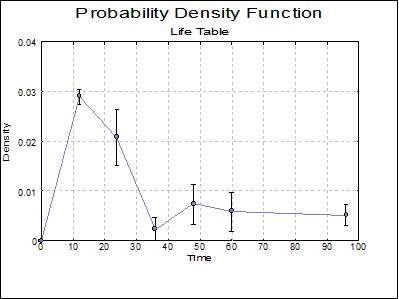
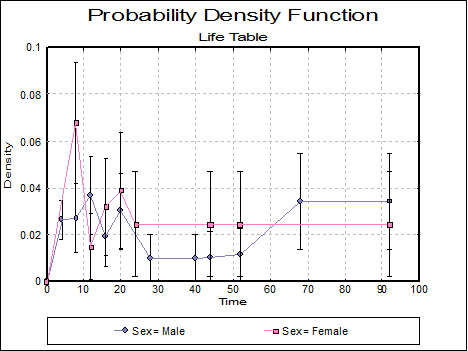
Plot of Probability Density: A plot of the probability density is displayed for each factor level. Select Error Bars in the Edit → Data Series dialogue to display standard errors or confidence intervals of the probability density function as error bars.

9.4.1.3. Life Table Example

Data on survival times of patients in a study on multiple myeloma is given in Table 1.3, p. 9, in Collett, D. (1994). Examples 2.2 (p. 17) and 2.5 (p. 28) give the Life Table estimates and the plot of the survival and hazard functions for this data.

Open SURVIVAL and select Statistics 2 → Survival Analysis → Life Table. From the Variable Selection Dialogue select the data option 1 Enter Durations and Survival time (C10) as [Time] and Status (C11) as [Censored]. Enter the following two lines for the interval selection dialogue.

 

Interval Size	No of Intervals
12	5
36	1
0	0
0	0
0	0

Instead of entering 8 regular intervals of size 12, here we enter 5 intervals of size 12 and one interval of size 36. This is because the results given by Collett in Tables 2.1 and 2.4 are obtained by aggregating the last 3 intervals into one. Selecting Life Table and checking all output options in the next two dialogues, the following results are obtained:

Life Table

Time Variable: Survival time

Censor Variable: Status

Number of Cases Censored: 12 ( 25.0%)

Valid Number of Cases: 48, 0 Omitted

Median Survival Time = 19.2800

 

Interval Start	Number Entering	Number Censored	Number Exposed	Number Terminating	Proportion Surviving	Cumulative Proportion Surviving
0	48	4	46.0	16	0.6522	0.6522
12	28	4	26.0	10	0.6154	0.4013
24	14	0	14.0	1	0.9286	0.3727
36	13	1	12.5	3	0.7600	0.2832
48	9	2	8.0	2	0.7500	0.2124
60	5	1	4.5	4	0.1111	0.0236

 

Interval Start	Std Error Cumulative Surviving	Lower 95% Cumulative Surviving	Upper 95% Cumulative Surviving	Proportion Terminating	Cumulative Proportion Terminating	Std Error Cumulative Terminating
0	0.0702	0.4964	0.7704	0.3478	0.3478	0.0702
12	0.0758	0.2543	0.5440	0.3846	0.5987	0.0758
24	0.0756	0.2284	0.5169	0.0714	0.6273	0.0756
36	0.0730	0.1522	0.4294	0.2400	0.7168	0.0730
48	0.0698	0.0955	0.3598	0.2500	0.7876	0.0698
60	0.0324	0.0005	0.1610	0.8889	0.9764	0.0324

 

Interval Start	Lower 95% of Cumulative Terminating	Upper 95% of Cumulative Terminating	Hazard Rate	Std Error of Hazard Rate	Lower 95% of Hazard Rate	Upper 95% of Hazard Rate
0	0.2296	0.5036	0.0351	0.0086	0.0183	0.0519
12	0.4560	0.7457	0.0397	0.0122	0.0158	0.0636
24	0.4831	0.7716	0.0062	0.0062	0.0000	0.0183
36	0.5706	0.8478	0.0227	0.0130	0.0000	0.0482
48	0.6402	0.9045	0.0238	0.0167	0.0000	0.0565
60	0.8390	0.9995	0.0444	0.0133	0.0183	0.0706

 

Interval Start	Probability Density	Sta Error Probability Density	Lower 95% of Probability Density	Upper 95% of Probability Density
0	0.0290	0.0015	0.0261	0.0319
12	0.0209	0.0057	0.0098	0.0320
24	0.0024	0.0023	0.0000	0.0070
36	0.0075	0.0040	0.0000	0.0154
48	0.0059	0.0039	0.0000	0.0136
60	0.0052	0.0019	0.0015	0.0090