3.4. Formula
Columns may be defined as functions of other columns. A function returns in the nth row of the current column the function evaluation of the nth rows of columns in its argument.
In order to enter a simple formula simply press <=> or select Formula → Quick Formula. For more complex formulas select Formula → Formula Editor, which will provide full information on the options available.
3.4.0. Overview
3.4.0.1. Entering Formulas
To enter a formula, position the active cell at any row of the destination column (empty or used) and select Formula → Quick Formula. If the formula is to be defined, say, for column 4, then a text box will be placed on the Input Panel already containing C4 = . Type in the right hand side of the formula followed by <Enter/OK>. The formula will be computed immediately and results placed in column 4. Any combination of upper and lower case letters can be used.
In the above example, although the text box appears with C4 = , the current column placed on the left hand side of the equation, you can edit this to send the results to any other column you choose. For instance, if you enter C10 = C1 * C2 then the results will be sent to column 10 regardless of the initial active cell position. Examples given in the following sections will omit the left hand side of formulas, which means that the results are put into the current column.
There are two ways of referring to a column in functions. If column n has the label Label, then it may be referred to as either Cn or Label. For example, to define every row of column 4 as the square of every corresponding row of column 2, the formula can be written either as:
C2^2
or as:
Label^2
3.4.0.2. Computing a Range of Formulas
When you need to compute the same formula over a range of columns, first enter the formula as normal, and then append the number of times it should be repeated preceded by a hash sign #. The column numbers in the formula will be incremented by one each time the formula is computed for a new column. For instance, if you enter the following when the active cell is on column 4:
C2#3
then column 2 will be copied to column 4, column 3 to column 5, and column 4 to column 6. In this example, the final contents of columns 2, 4 and 6 will be the same, as the column numbers in the function will be incremented irrespective of this being the end result of a previous function evaluation or not. Incrementing will work regardless of the original position of the active cell, such that it is possible to redefine columns in their own places. Suppose there is data from C1 to C6 in the Data Processor and you wish to take their logarithms. Suppose also that there is no need to retain the original numbers. Then all you have to do is to place the active cell on any row of column 1, select Formula → Quick Formula and enter the following:
Log(C1)#6
You may not always want all column numbers in a function incremented. For instance, to multiply one column with all other columns in a range you must be able to keep this column fixed while the others are incremented. This is done by prefixing such columns by a $ sign:
C4+$C2*Log(C1)#6
In this example columns C4 and C1 will be incremented but C2 will remain fixed.
Any type of formulas which will be discussed in the following sections can be computed over a range in this way.
3.4.0.3. Using Column Labels in Formulas
UNISTAT imposes no restrictions on the use of Column Labels in formulas, but you must realise that you are not absolutely free to use any column label in a formula. Suppose, for example, you want to compute the following:
C1/Sqr(C1+3)
If the label of C1 is S and you want to use this label rather than the column number in the formula, then it should look like this:
S/Sqr(S+3)
In this case the program will consider the letter S in Sqr() as another occurrence of the column label S and then report a Syntax error. You must ensure that no Column Labels used in formulas are a subset of the function strings used by the Data Processor. The function compilation is case sensitive; that is, lower and upper case letters are distinguished by the program. If, for instance, in the above example the column label were s (i.e. lower case) and the formula were written in the same way, i.e.:
s/Sqr(s+3)
there would be no confusion. Therefore, if you avoid entering both labels and function strings in the same case (i.e. both lower or both upper case) the problem will never arise. Of course another alternative is to avoid using Column Labels shorter than four characters. Then there will be no scope for confusion.
3.4.0.4. Formula Syntax
If a formula is entered improperly, then the program will display the prompt Syntax error and then reactivate the formula input field to enable you to edit the input string immediately. It is possible to leave the input field by pressing <Escape/Cancel>. Note, however, that the existence of wrong formulas in the data matrix will generate further error messages when the Compute Matrix procedure is used subsequently. Thus it is recommended that the wrong formulas are either corrected or converted to Data (see 3.4.2.6.1. Data Conversion Functions) or deleted.
All spaces can be omitted from a formula string. This is in fact what the program does before processing a formula input. Formulas are calculated immediately after they are entered. If a change is made in a data column which is used as one of the arguments of a formula, the formula values will not be updated automatically. All formulas in the data matrix can be updated by selecting Formula → Compute Matrix.
Scalar Functions: If a column is defined as a function of scalars only, then the program will fill all cells with the same scalar value of the function up to the maximum row used (see 3.4.2.4. Scalar Functions).
Missing Values: If there is missing data in at least one of the argument columns then the corresponding row of the function value will be missing.
Unequal Column Lengths: If a combination of columns with unequal lengths is used in a formula, the rows of the resultant column above the shortest length will be treated as missing.
3.4.0.5. Converting Formula Columns into Data
When a column is defined as a formula, then data entry, editing, deleting, etc. are not allowed in this column. To do this, you can redefine the column as data by setting its formula to Data (see 3.4.2.6.1. Data Conversion Functions). Suppose, for instance, column 2 is defined as natural logarithm of column 1:
C2 = Lne(C1)
To convert C2 into a numeric data column you can press the equal key <=> again while the active cell is somewhere on C2 and enter one of the following two functions:
Data
Number
This will delete the formula in column 2 and its entries can be overwritten, deleted or new data points appended.
3.4.1. Quick Formula
If you are sure about the syntax of the formula you wish to enter, then select this option. Otherwise, use the Formula → Formula Editor option which is described below.
The short key for Quick Formula is the equal key <=>.
3.4.2. Formula Editor
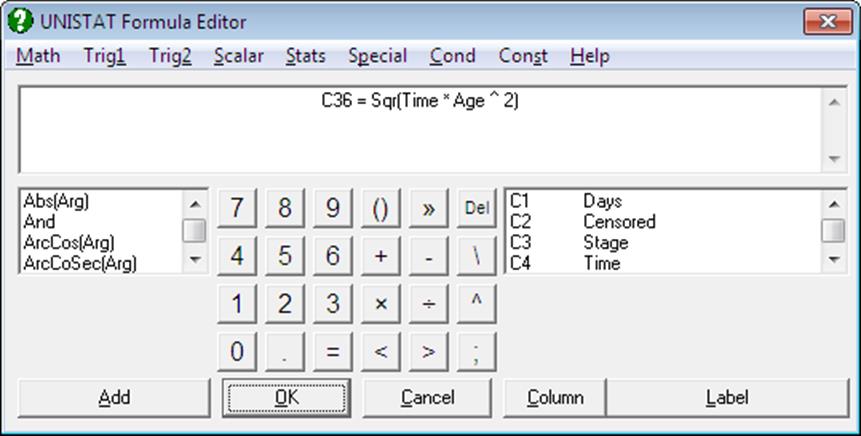
Formulas can be typed into Input Panel or the Formula Editor can be used to build a formula. In Data Processor, you can access this dialogue from Formula → Formula Editor. In other parts of the program, where you are asked to supply a formula (like Plot of Functions or Nonlinear Regression) double-clicking on a formula text box will activate the Formula Editor. The options available on this dialogue will be different in different parts of the program.
3.4.2.0. Overview
You can build a formula with the Formula Editor without using the keyboard. All numbers, operators, formulas and variable names are available on buttons, in lists or from the pull down menus. If the formula is too long it will be split over a number of lines which are displayed at the top of the Formula Editor.
1) The menu bar provides access to all available functions which are grouped into relevant categories. When you make a selection from a menu list as usual, the text for the selected item will be pasted into the formula text field.
2) A list situated on the left of the window also provides access to all functions which are sorted in alphabetical order. When you highlight an item and then click the [Add] button under the list, the text for the selected item will be pasted into the formula at the cursor position.
3) Another list situated on the right of the window displays all spreadsheet columns containing data (i.e. the variables). First highlight the desired column in the list. In order to paste the column reference by number (i.e. C1, C5, etc.) click on the [Column] button. If the column has a label, you may click on the Label button to paste the label of the column (e.g. Time, Fixed Capital) into the formula.
3.4.2.1. Mathematical Operators and Functions
Any expressions (including columns and arithmetic expressions) can be supplied as arguments of functions. String variables cannot be arguments of such functions.
Operators: The following mathematical operators can be used in formulas:
|
+ |
add |
|
– |
subtract |
|
* |
multiply |
|
/ |
floating point divide |
|
^ |
power |
|
\ |
integer divide; divides two numbers and returns only the integer part |
|
Mod |
divides two numbers and returns only the remainder |
Exp(): Returns the exponential of its argument. This is e raised to the power of arg, which is the inverse of log to base e. If arg takes on a value which is outside the range -700 to 700, then an Argument Error message is issued and the procedure is terminated.
Syntax:
Exp(arg)
Examples:
Exp(C1*2*Sqr(C2))
Exp(Label1^2/Lne(Label2))
Log(): Returns the log to base 10 of its argument. If arg takes on a non positive value, then an Argument Error message is issued and the procedure is terminated.
Syntax:
Log(arg)
Examples:
Log(C1*2* Sqr(C2))
Log(Label1^2/10^Label2)
Lne(): Returns the log to base e of its argument. The log to base N of x is given by Lne(x)/Lne(N). If arg takes on a non positive value, then an Argument Error message is issued and the procedure is terminated.
Syntax:
Lne(arg)
Examples:
Lne(Exp(C1)/2)
Lne(Label1^2)
Sqr(): Returns the square root of its argument. If arg takes on a negative value, then an Argument Error message is issued and the procedure is terminated.
Syntax:
Sqr(arg)
Examples:
Sqr(C1*C2)
Sqr(Label1^3)
Fct(): Returns the factorial of its argument when the argument is a positive integer m, where 0 ≤ m ≤ 169. If arg is a positive decimal number, then the gamma function of arg +1 is returned. The gamma function of x+1 is equal to the factorial of x when x is a positive integer.
Syntax:
Fct(arg)
Examples:
Fct(Rno)
Fct(25)/(Fct(12)*Fct(13))
Fct(3.5)
The last example will return the scalar 11.631728.
Int(): Returns the integer part of its argument, rounding it down.
Syntax:
Int(arg)
Examples:
Int(Sqr(C1/2))
Int(Label1^1.234)
Abs(): Returns the magnitude of its expression. For positive values this is the value itself and for negative values -1 times the value.
Syntax:
Abs(arg)
Examples:
Abs(C1/C2)
Abs(Int(Label1))
Sgn(): Returns +1 if arg is positive, 0 if arg is zero and -1 if arg is negative.
Syntax:
Sgn(arg)
Examples:
Sgn(C1*C2)
Sgn(Label1)
3.4.2.2. Trigonometric Functions 1
Angular arguments of all trigonometric functions must be expressed in radians.
1 radian = 180/Pi() degrees.
Sin(): Returns the sine of its argument.
Cos(): Returns the cosine of its argument.
Tan(): Returns the tangent of its argument.
Sec(): Returns the secant of its argument. The secant of arg is equal to the inverse cosine of arg:
Sec(arg) = 1/Cos(arg).
CoSec(): Returns the cosecant of its argument. The cosecant of arg is equal to the inverse sine of arg:
CoSec(arg) = 1/Sin(arg).
CoTan(): Returns the cotangent of its argument. The cotangent of arg is equal to the inverse tangent of arg:
CoTan(arg) = 1/Tan(arg).
ArcSin(): Returns the inverse sine of its argument.
-1 ≤ arg ≤ 1.
ArcCos(): Returns the inverse cosine of its argument.
-1 ≤ arg ≤ 1.
ArcTan(): Returns the inverse tangent of arg.
-1E300 ≤ arg ≤ 1E300.
ArcSec(): Returns the inverse secant of arg.
-1E300 ≤ arg ≤ 1E300.
ArcCoSec(): Returns the inverse cosecant of arg.
-1E300 ≤ arg ≤ 1E300.
ArcCoTan(): Returns the inverse cotangent of arg.
-1E300 ≤ arg ≤ 1E300.
3.4.2.3. Trigonometric Functions 2
These are the hyperbolic trigonometric functions.
Angular arguments of all trigonometric functions must be expressed in radians.
1 radian = 180/Pi() degrees.
HSin(): Returns the hyperbolic sine of its argument.
HCos(): Returns the hyperbolic cosine of its argument.
HTan(): Returns the hyperbolic tangent of its argument.
HSec(): Returns the hyperbolic secant of its argument. The secant of arg is equal to the inverse hyperbolic cosine of arg:
HSec(arg) = 1/ HCos(arg).
HCoSec(): Returns the hyperbolic cosecant of its argument. The cosecant of arg is equal to the inverse hyperbolic sine of arg:
HCoSec(arg) = 1/HSin(arg).
HCoTan(): Returns the hyperbolic cotangent its argument. The cotangent of arg is equal the inverse hyperbolic tangent of arg:
HCoTan(arg) = 1/HTan(arg).
HArcSin(): Returns the inverse hyperbolic sine of its argument.
HArcCos(): Returns the inverse hyperbolic cosine of its argument.
HArcTan(): Returns the inverse hyperbolic tangent of its argument.
HArcSec(): Returns the inverse hyperbolic secant of its argument.
HArcCoSec(): Returns the inverse hyperbolic cosecant of its argument.
HArcCoTan(): Returns the inverse hyperbolic cotangent of its argument.
3.4.2.4. Scalar Functions
These functions return scalar values about their argument columns. If only Scalar Functions are used in the definition of a column then the column will be filled with the same scalar value up to the maximum row used. The argument of a scalar function can only be a single column, i.e. either a column number Cn or a column label.
If the type of the argument column is one of String, Date or Time, then only the Len(), Mis(), Min(), Max() functions will return nonmissing values.
Len(): Number of observations in column n (including missing observations).
Syntax:
Len(Cn)
Len(Label)
Mis(): The number of missing observations in column n.
Syntax:
Mis(Cn)
Mis(Label)
Avg(): The mean of column n (adjusted for missing values).
Syntax:
Avg(Cn)
Avg(Label)
Std(): The sample standard deviation of column n (adjusted for missing values) with Len(Cn)– Mis(Cn)-1 degrees of freedom.
Syntax:
Std(Cn)
Std(Label)
Ser(): The standard error, i.e. standard deviation divided by the square root of the valid number of cases (adjusted for missing values) with Len(Cn)– Mis(Cn)-1 degrees of freedom.
Syntax:
Ser(Cn)
Ser(Label)
Var(): The sample variance of column n (adjusted for missing values) with Len(Cn)– Mis(Cn)-1 degrees of freedom.
Syntax:
Var(Cn)
Var(Label)
Sum(): The sum of observations in column n.
Syntax:
Sum(Cn)
Sum(Label)
Ssq(): The sum of squares of observations in column n.
Syntax:
Ssq(Cn)
Ssq(Label)
Min(): The smallest observation in column n.
Syntax:
Min(Cn)
Min(Label)
Max(): The largest observation in column n.
Syntax:
Max(Cn)
Max(Label)
3.4.2.5. Statistical Functions
These are some of the most commonly used Statistical Functions. They must be used as individual functions and should not form a part of a larger formula. Also, their argument can only be a single column (i.e. either a column number Cn or a column label).
These functions are only available in the Data Processor.
Sort(): Sorts a column Cn and places the results in the current column. If D is appended to the end (following a semicolon) then the sort will be in descending order.
Syntax:
Sort(Cn)[;D]
Examples:
Sort(C1)
Sort(C1);D
Sort(Label)
Sort(Label);D
Missing data are treated as ordinary numbers, having the value displayed in Tools → Options → Memory Management. This function is in effect identical to Data → Column Sort option. Its main advantage is, however, that it keeps the source column unchanged when the source and destination columns are different.
Rank(): Computes the ascending ranks of a column of numbers or strings and places the results in the current column. The source column and the destination column cannot be the same. If the character D is appended to the end (following a semicolon) then the descending ranks are computed. Equal observations are assigned their average rank.
Syntax:
Rank(Cn)[;D]
Examples:
Rank(C1)
Rank(C1);D
Rank(Label)
Rank(Label);D
Cumul(): Computes the cumulative values of a column. If R is appended to the end (following a semicolon) then the relative cumulative values are calculated; i.e., values will be divided by the column sum.
Syntax:
Cumul(Cn)[;R]
Examples:
Cumul(C1)
Cumul(C1);R
Cumul(Label)
Cumul(Label);R
Mova(): Computes the m order moving averages of column Cn and places the results in the current column.
Syntax:
Mova(Cn;m)
Examples:
Mova(C3;5)
Mova(Label;8)
Round(): Rounds off the values of column Cn to m decimal places and places the results in the current column. This is different from the Data → Format Columns option in that it actually changes the values stored in memory. Format affects only the display of numbers.
Syntax:
Round(Cn;m)
Examples:
Round(C3;2)
Round(Label;0)
Stan(): Standardises the values of column Cn using its mean and sample standard deviation and places the results in the current column. The resultant column will have a zero mean and unit variance.
Syntax:
Stan(Cn)
Example:
Stan(C3)
Stan(Label)
Level(): This function is used to generate a balanced factor column with integer entries. The argument n is a positive integer and the column is filled with recurring sequences of integers from 1 to n, up to the maximum column length, using the formula ((n – 1) Mod J + 1). If the optional argument B is used, the column is filled a sequence of n-integer blocks using the formula (Int((n – 1) / J) + 1).
Syntax:
Level(n)[;B]
Examples:
Level(3): Fills the column with 1 2 3 1 2 3 1 2 3 1 2 3 …
Level(2);B: Fills the column with 1 1 2 2 3 3 4 4 …
Dummy(): This function is used to create n new columns (dummy variables) for a factor column with n levels (its argument), each of which corresponding to a level. A case in a dummy column will have the value of 1 if the factor contains the corresponding level in the same row, and 0 otherwise.
The Dummy() function also accepts two options, F and L, which will omit the first or last level respectively and generate n – 1 new columns. This may be desirable to remove the multicollinearity caused by inclusion of all levels, since dummy variables created in this way will always add up to the unit vector.
Dummy variables can also be created for interaction terms of up to three factors. Options F and L are also applicable to interaction terms.
The first of the dummy columns generated will be put in the current column (i.e. where the active cell is), which should not be one of the argument columns. Ensure that there are enough empty columns in the Data Processor, as the number of columns generated may be very large, especially when dummies are created for interactions.
Syntax:
Dummy(Cm[*Cn[*Co]])[;F][;L]
Examples:
Dummy(C3)
Dummy(Region);L
Dummy(Region*Type*Country);F
Freq(): Creates two new columns of length n for a (factor) column, which contains n distinct values (levels) and places the results in the current and the following column. The first new column contains the levels of the factor column and the second the number of times each level occurs.
Syntax:
Freq(Cn)
Example:
Freq(C3)
Freq(Label)
MdRk(): The exact median ranks are generated from the binomial function:
![]()
where N, the population size, should be supplied by the user and Ri is the median rank of the ith row. For large values of N not all exact median ranks can be computed and will be reported as missing values.
Syntax:
MdRk(N)
Example:
MdRk(85)
3.4.2.6. Special Functions
3.4.2.6.1. Data Conversion Functions
In order to understand the way these functions work, it is essential to remember that cells in Data Processor contain eight bytes of information. UNISTAT can interpret these eight bytes as a double precision floating number, eight characters of String Data (see 3.0.2.2.1. Short Strings), dates with days of the week and time including hours, minutes and seconds. The long String Data type (see 3.0.2.2.2. Long Strings) is a fundamentally different one requiring the long strings to be stored in a separate table (see 3.0.2.2. String Data and Long String Table).
It should be noted here that although these functions are extremely useful in some advanced data manipulations, their use is not needed under normal operating conditions.
Data or Number: When a column is defined as a formula column, its cells cannot be edited. Use this function to convert a formula column into a data column. Values in the cells will not change.
Data and Number can be used as alternatives but they cannot be used as part of a larger function. The first four characters are sufficient.
Syntax:
Data
Numb
Examples:
Data
Number
This function can also be used to convert a short string column into numbers. In this case, the 8-byte character data in each cell will be converted to its 8-byte floating point equivalent. Therefore, the outcome may not have any resemblance to original strings. To restore the short strings use the String function.
When used on a long string column, this function will convert Long Strings into their underlying integer values. The strings in Long String Table will not be deleted. To restore the long String Data use the Long() function.
String or Character: Converts numeric data columns into short strings. Strings longer than 8 characters are truncated. String or Character can be used as alternatives but they cannot be used as part of a larger function. The first four characters are sufficient. Also see 3.0.2.2. String Data.
Syntax:
Stri
Char
Examples:
String
Character
This function only converts 8-byte numbers to their 8-byte string equivalents. Therefore, the outcome may not have any resemblance to the original numbers. This function is only useful in restoring a short string column which has been converted into numbers using the Data function. You can also convert a long string column into short strings using the Short function, and a short string column into Long Strings using the Long function.
Short: Converts a numeric or long string column into a short string column. It cannot be used as part of a larger function. and the first four characters are sufficient.
Syntax:
Short
Examples:
Short
Although the Long String Table entries of the original long string column are not deleted, its underlying integers are lost.
Long: Converts a numeric or short string column into a long string column, creating a Long String Table column in the process. It cannot be used as part of a larger function.
Syntax:
Long
Examples:
Long
The short string columns converted into long using this function can be restored using the Short function.
Long(n): Converts numeric data columns containing integers into long string columns, establishing a correspondence between the current column and the column of the Long String Table referenced in its argument. The Long String Table is assumed to be populated earlier. This function cannot be used as part of a larger function. Also see 3.0.2.2. String Data.
Syntax:
Long(n)
Examples:
Long(3)
This function will not convert a short string column into a long string one. To do this use the Long function.
Date: Converts function or numeric data columns into Date Data. This function cannot be used as part of a larger formula.
Syntax:
Date
Example:
Date
Time: Converts function or numeric data columns into Time Data. This function cannot be used as part of a larger formula.
Syntax:
Time
Example:
Time
3.4.2.6.2. Date and Time Functions
Days(): This function is used to fill a column with dates. The user is expected to supply an initial date. The function will then automatically increment rows at one day intervals. Optionally, a second argument can be supplied separated by a semicolon. When N is a positive integer days will be incremented by N days at a time. N may also take negative values, -1, -2, -3, to create the following effects:
-1: Working days, Monday to Friday.
-2: 6-day week, Monday to Saturday.
-3: Weekend days, Saturday and Sunday.
Syntax:
Days(Date)
Days(Date;N)
Examples:
Days(12/12/1990)
Days(5/11/1984;7)
Days(7/4/82;-1)
Hour(): This function is used to fill a column with Time Data. The user is expected to supply an initial time. The function will then automatically increment rows at one hour intervals. Optionally, a second argument can be supplied separated by a semicolon. When N is a positive integer, time will be incremented by N hours at a time.
The Hour() function returns the data type Time and it cannot be used as part of a larger formula. If you want a step length which is a fraction of an hour, then use one of Mins() or Secs() functions.
Syntax:
Hour(Time)
Hour(Time;N)
Examples:
Hour(0:0)
Hour(10:00:00;2)
Mins(): This function is used to fill an entire column with Time Data. The user is expected to supply an initial time. The function will then automatically increment rows at one minute intervals. Optionally, a second argument can be supplied separated by a semicolon. When N is a positive integer, time will be incremented by N minutes at a time.
The Mins() function returns data type Time and it cannot be used as part of a larger formula. If you want a step length which is a fraction of a minute, then use the Secs() function.
Syntax:
Mins(Time)
Mins(Time;N)
Examples:
Mins(0:0)
Mins(0:1:0;3)
Mins(1:00:00;10)
Secs(): This function is used to fill an entire column with Time Data. The user is expected to supply an initial time. The function will then automatically increment rows at one second intervals. Optionally, a second argument can be supplied separated by a semicolon. When N is a positive integer, time will be incremented by N seconds at a time.
The Secs() function returns data type Time and it cannot be used as part of a larger formula.
Syntax:
Secs(Time)
Secs(Time;N)
Examples:
Secs(0:0)
Secs(0:1;30)
Secs(1:10:10;100)
3.4.2.6.3. UNISTAT Functions
Select: Selects and deselects a Select Row column. The first four characters are sufficient. This is equivalent to selecting Data → Select Row from the Data Processor menu (see 3.3.12. Select Row).
Reg: Computes the fitted values for an estimated regression equation.
Syntax:
Reg
Example:
Reg
This is a powerful prediction and interpolation tool and is used in conjunction with the following procedures:
|
Data and Function plots |
X-Y Curve fitting options |
Polynomial |
|
|
|
Geometric |
|
|
|
Exponential |
|
|
X-Y-Z Surface fitting options |
Plane |
|
|
|
Polynomial surface |
|
Regression and ANOVA: |
Linear regression |
|
|
|
Polynomial regression |
|
This function can only be used immediately after fitting a curve or running a regression in one of the procedures listed above. If you return to the Data Processor after running a regression, then the program will hold the regression variable list and the regression coefficients in its memory. Placing the active cell on an empty column and entering the function Reg, the fitted values can be recomputed.
The Reg function allows performance of prediction and what if scenarios by adding new observations to the regression variables or changing their values respectively. The Reg function will not work properly if the positions of the regression variables in the data matrix are changed or other procedures are executed after running a regression.
Geometric and exponential fits or any other curve fitting options with one or more logarithmic axes will generate coefficients for the transformed variables. In such cases it is left to the user to transform the fitted results back to the original coordinates by using the necessary Data Processor functions (like Exp()). Also remember that coefficients for the fitted equation will be saved in the file POLYCOEF.TXT (see 4.1.1.2. Curve Fitting and 4.2.1.5. Surface Fitting).
Rnd(): Generates Random Numbers between 0 and 1, with seed m.
Syntax:
Rnd(m)
Example:
Int(100*Rnd(-1))
You can also generate Random Numbers conforming to a number of Distribution Functions in Descriptive Statistics module.
Rno: Returns the row number of the cell.
Syntax:
Rno
Example:
1899+ Rno
Row(): Returns the value of the mth previous row of the current column.
Syntax:
Row(-m)
This function allows the user to perform a variety of row operations. It is possible to mix more than one lag within one formula, including Row(0) which returns the value of the current row. Positive integers cannot be used. The user must provide as many initial values as the highest number of lags. The function will start computing with the row number corresponding to the highest lag value.
Examples:
Row(-1)
If the first cell of the current column contains 1, then this will return the row numbers just like the function Rno.
Row(-3)*Sqr(Row(-1)/2)+ Row(0)
In this case the first three rows of the current column must contain numbers.
WARNING! The Row() function must be used with care. Operations containing exponentiation or multiplication may quickly result in a number overflow.
3.4.2.7. Conditional Functions
Complex Conditional Functions can be computed by means of the If() function.
Syntax:
If(arg1); arg2; arg3
where:
arg1 is a logical condition,
arg2 is returned when arg1 is true, and
arg3 is returned when arg1 is false.
Any combination of the following logical operators can be used to construct the logical condition arg1:
And: Bitwise And operator. e.g. 7 And 14 = 6, True And False = False.
Or: Bitwise Or operator. e.g. 7 Or 14 = 15, True Or False = True.
Not(arg): Returns the bitwise Not() of arg. e.g. Not(1) = -2, Not(True) = False. Use of parentheses in Not() is compulsory (without a space between Not and the left parenthesis).
arg2 and arg3 can be mathematical expressions containing functions, scalars or missing values.
The If() function and use of logical operators are only available in the Data Processor.
Examples:
If(C1>C2);C1;C2
If(C1+C2>100);C1^2-2;C1^3+3
If(C3>0 Or Not(C2<5));*;Rno
If(Label>1 And Label<2);Label;*
Columns containing String Data can also be used as arguments of an If() function. When a particular value is referred to, it should be enclosed within single quotes:
If(C3>‘England’ Or C2=‘Scotland’);*;C2
If(Label>1 And Label<2); ‘Yes’;‘No’
String Data are compared according to their alphabetical ordering.
3.4.2.8. Constants
These functions return the commonly used constants in formulas.
Missing Value: This returns UNISTAT’s internal missing value code as displayed in Data Processor’s Tools → Options dialogue (see 2.4.1.1. Memory Management).
Pi(): Returns the value 3.14159265358979.
e(): Returns the value 2.71828182845905.
3.4.3. Compute Matrix
This option is used for updating formulas after changes have been made in their argument data columns. If changes have been made in columns containing data and if these are used as arguments of a formula (directly or indirectly), then values of the function can be updated by selecting Formula → Compute Matrix.
3.4.4. Calculate
Any calculations involving scalars can be performed. It is also possible to include the Data Processor’s Scalar Functions Len(), Mis(), Avg(), Var(), Std(), Ser(), Sum(), Ssq(), Min() and Max() in expressions.
After writing the expression press <Enter/OK> once to display the result. Pressing it once again will enter this value in the active cell. Pressing any other key will clear the Input Panel.
