6.7.3. Variance
6.7.3.1. Sample Size for Variance
The relationship between the estimates of sample and population variances is given as follows:
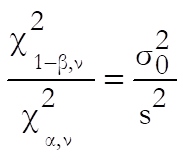
Here:
·
is the estimate of the
population variance,
·
is the sample variance with ν
degrees of freedom,
· α is the probability of committing a Type I error and 1- α is the confidence level,
· β is the probability of committing a Type II error and 1 – β is the power of the test,
Since critical values from chi-square distribution are both dependent on the sample size n, an iterational algorithm should be employed.
The user is expected to enter:
· Sample Variance
· Population Variance
· Power of the test
· Confidence Level
and the program will output the estimated sample size.
Example
Example 7.12 on p. 124 from Zar, J. H. (2010). Select Statistics 1 → Sample Size and Power Estimation → Variance and the Sample Size option. Enter the following data at the next dialogue:
Sample Size and Power Estimation: Variance
Sample Size
|
Sample Variance = |
2.6898 |
|
Population Variance = |
1.5000 |
|
Power of the Test = |
0.9000 |
|
Confidence Level = |
0.9500 |
|
Estimated Sample Size = |
50.7813 |
6.7.3.2. Power of the Test for Variance
Power of the test is defined as the following probability:
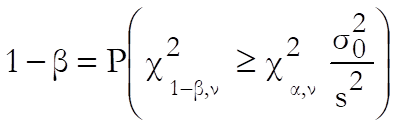
Since the first chi-square value on the right hand side of this equation depends on β, an iterational algorithm should be employed.
The user is expected to enter:
· Sample Size
· Sample Variance
· Population Variance
· Confidence Level
and the program will output the estimated chi-square statistic and its p-value, β.
Example
The example on p. 124 from Zar, J. H. (2010). Select Statistics 1 → Sample Size and Power Estimation → Variance and the Power of the Test option. Enter the following data at the next dialogue:
Sample Size and Power Estimation: Variance
Power of the Test
|
Sample Size = |
8.0000 |
|
Sample Variance = |
2.6898 |
|
Population Variance = |
1.5000 |
|
Confidence Level = |
0.9500 |
|
Power of the Test: |
|
|
Chi-Square Statistic = |
7.8447 |
|
Right-Tail Probability = |
0.3465 |