6.7.4. Correlation
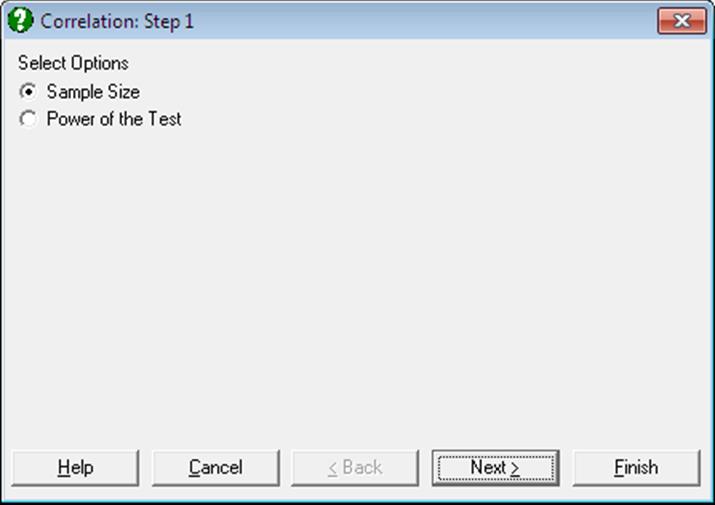
6.7.4.1. Sample Size for Correlation
The sample size is estimated using the following formula:
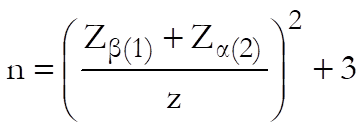
where:
· and z is the Fisher’s z transformation of the correlation coefficient r,
·
is the one-tailed critical
value from the standard normal distribution,
·
is the (one or) two-tailed
critical value from the standard normal distribution.
The user is expected to enter:
· Correlation Coefficient
· Power of the test
· Confidence Level
· 1 or 2 tailed test
and the program will output the estimated sample size.
Example
Example 19.5a on p. 388 from Zar, J. H. (2010). Select Statistics 1 → Sample Size and Power Estimation → Correlation and the Sample Size option. Enter the following data at the next dialogue:
Sample Size and Power Estimation: Correlation
Sample Size
|
Correlation Coefficient = |
0.5000 |
|
Power of the Test = |
0.9900 |
|
Confidence Level = |
0.9500 |
|
1 or 2 Tailed Test = |
2.0000 |
|
Estimated Sample Size = |
63.9136 |
6.7.4.2. Power of the Test for Correlation
Power of the test is one minus the p-value of the following Z-statistic:
where:
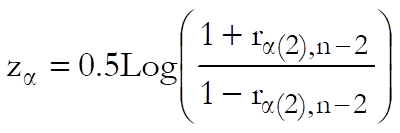
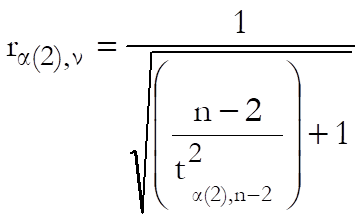
and 
is the (one or) two-tailed
critical value from t-distribution with n-2 degrees of freedom.
The user is expected to enter:
· Sample Size
· Correlation Coefficient
· Confidence Level
· 1 or 2 tailed test
and the program will output the estimated Z-statistic and its p-value.
Example
Example 19.4 on p. 388 from Zar, J. H. (2010). Select Statistics 1 → Sample Size and Power Estimation → Correlation and the Power of the Test option. Enter the following data at the next dialogue:
Sample Size and Power Estimation: Correlation
Power of the Test
|
Sample Size = |
12.0000 |
|
Correlation Coefficient = |
0.8700 |
|
Confidence Level = |
0.9500 |
|
1 or 2 Tailed Test = |
2.0000 |
|
Power of the Test: |
|
|
Z-Statistic = |
2.0300 |
|
2-Tail Probability = |
0.9788 |