6.2.3. Partial Correlation Matrix

Partial correlation is used to obtain the linear correlation between two variables after the effects of some other variables are filtered out. The latter are referred to as control variables. The number of control quickly get complicated:

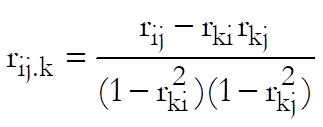
where i and j are the variables to be correlated and k is the control variable. All correlation coefficients on the right hand side of the equation are zero order (Pearson) Correlation Coefficients.

Like the Pearson-Spearman-Kendall Correlations Matrix procedure, Partial Correlation Matrix can compute more than one coefficient at a time and display the results in the form of a matrix. Each cell of the output matrix displays the correlation coefficient, number of cases and the probability. One or two-tailed probabilities can be displayed, as selected in the Pearson-Spearman-Kendall Correlations Matrix procedure.

Select the columns to be correlated from the Variable Available list by clicking on [Variable]. It is possible to select up to three control variables by clicking on [Control 1], [Control 2] and [Control 3] in the correct order. That is, for the first order correlations mark one column clicking on [Control 1], for the second order correlations mark two columns clicking on [Control 1] and [Control 2], etc. There is no need to specify the order of correlations separately as the program will get this information from the highest number of control variable selected. Accordingly, if no control variables are selected then the program will compute the zero order (i.e. Pearson) correlations.

The program will consider each pair of variables separately, and calculate coefficients for only those pairs with equal size. Output matrix cells for columns with unequal lengths will be left blank. Also, the program will handle missing values for each pair of columns separately and omit pairs of cases with at least one missing value.

Example

Example 20.2 on p. 439 from Zar, J. H. (2010). In this particular example, the partial correlation for each pair is computed using all the rest of the variables as controls. Here it will be sufficient to generate one of the partial correlation coefficients.

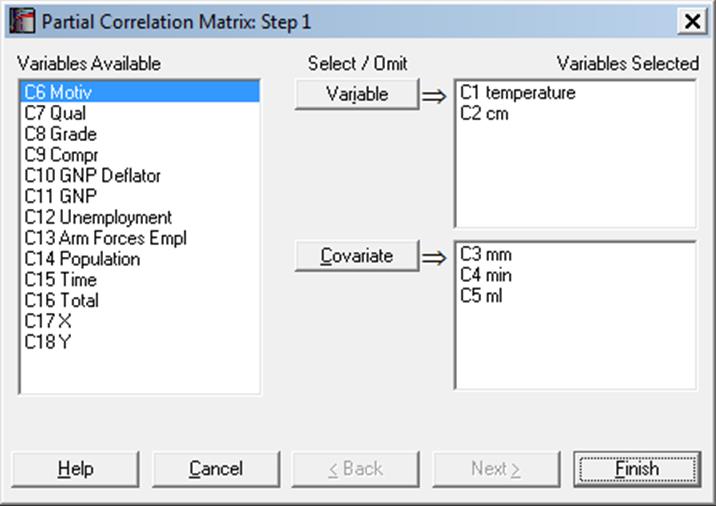
Open REGRESS, select Statistics 1 → Correlation Coefficients → Partial Correlation and select temperature (C1) and cm (C2) as [Variable]s and mm (C3) as [Control 1], min (C4) as [Control 2] and ml (C5) as [Control 3] to obtain the following results: