6.8.3. Summary of Effect Sizes
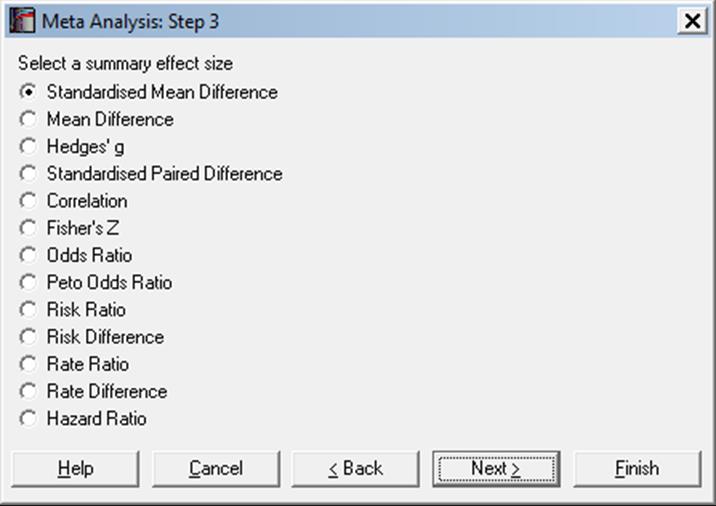
The summary effect size type is selected from the next dialogue. The program will estimate a fixed effect model and a random effects model for the mean effect size using a weighted average. By default, for each individual study the inverse of its variance is used as the weight for both models. It is also possible to select the Mantel-Haenszel weights for 2 x 2 tables.
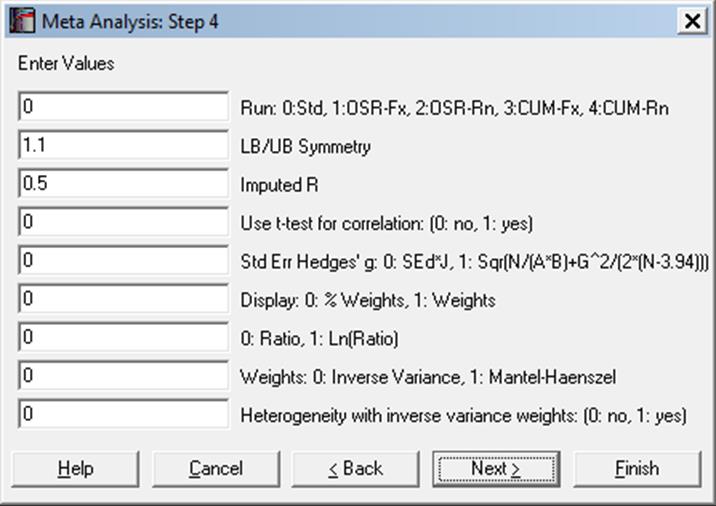
Run analysis:
0: Standard: Individual effect sizes and their standard errors are displayed with both fixed and random effects models.
1: One study removed with fixed effect: For each study, that study is removed and the fixed effect summary for the rest of the studies is displayed in its place.
2: One study removed with random effects
3: Cumulative with fixed effect: For each study, the fixed effect summary for all studies up to and including that study is displayed in its place. If the studies are already sorted in chronological order, then the cumulative analysis provides the summary effects of all studies known to a particular study on its publication date.
4: Cumulative with random effects
LB/UB Symmetry: When both lower and upper bounds are given for a confidence interval, they must be consistent with each other. UNISTAT will calculate the central tendency using both LB and UB. If the two values are within 10% of each other they will be deemed consistent and the results will be displayed. Otherwise, the current study will be reported as having invalid data. You can adjust the consistency level by entering a different multiplier.
Imputed r: Calculation of effect size for paired samples requires knowing the correlation between them. However, this may not be readily available in most studies. In such cases, the program assumes a correlation of 0.5 by default. This value can be changed by the user. See section 6.8.2.4. Paired Samples for details.
Use t-test for correlation: If the t-statistic was originally reported for a study based on the correlation coefficient, then enter a non-zero value for this box. See section 6.8.2.4. Paired Samples for details.
Standard Error for Hedges’ g: You can choose one of two alternative methods for calculating the standard error of Hedges’ g. See section 6.8.2.3. Unpaired Samples for details.
Display relative or absolute weights: In Results and Forest Plot output, the weights can be displayed as relative weights in percentage terms or as absolute weights as used in calculations.
Ratio or Log(Ratio): This option will be available when one of odds, Peto odds, risk, rate and hazard ratio is selected as the summary effect size.
Weights: Inverse Variance or Mantel-Haenszel: The inverse variance method is the default for all types of effect size. Mantel-Haenszel weights can be calculated for the fixed effect model when one of odds or risk ratios or risk difference is selected as the summary effect size.
Heterogeneity with inverse variance weights: When Mantel-Haenszel weights are selected, the heterogeneity statistics are calculated with Mantel-Haenszel weights by default (see 6.8.4.2. Tests). You can, however, override this and force using inverse variance weights.
6.8.3.1. Fixed Effect Model
Inverse variance method
The weighted mean of individual effect sizes M is calculated as:
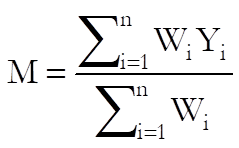
where the weight Wi is the reciprocal of the effect size variance Vi for a study:
![]()
and the variance of the mean effect size M is:
![]()
The Z-statistic is:
![]()
The relative weights are:
![]()
and the standardised residuals:
![]()
Mantel-Haenszel method for 2 x 2 tables
Odds ratio:
The summary odds ratio calculated as:
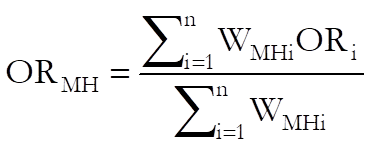
where the Mantel-Haenszel weight WMHi is:
![]()
and the variance Ln(ORMH) is:
![]()
where:
![]()
![]()
![]()
![]()
![]()
![]()
Risk ratio:
The Mantel-Haenszel weight WMHi is calculated as:
![]()
and the variance Ln(RRMH) is:
![]()
where:
![]()
![]()
![]()
Risk difference:
The Mantel-Haenszel weight WMHi is:
![]()
and the variance Ln(RDMH) is:
![]()
where:
![]()
![]()
6.8.3.2. Random Effects Model
Define the between-studies variance as introduced by DerSimonian R, Laird N. (1986):
![]()
where df = n – 1, Cochran’s Q is:
![]()
and:
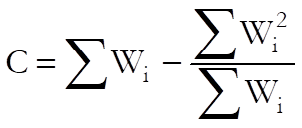
Next, determine the total variance for each study as the sum of within-study variance Vi and the between-studies variance of τ2:
![]()
The mean effect size, its variance, relative weights and standardised residuals are then computed as in the inverse variance method.
