6.8.4. Output Options
The first two output options have further selections.
6.8.4.1. Results
By default, only the effect size, its confidence limits and a character forest diagram are included in the output. Summary effects with fixed and random effects models are also displayed at the bottom of the table. It is possible to output the weights used for each model and residuals.
6.8.4.2. Tests
Tests for Heterogeneity
Cochran’s Q: As already defined in section 6.8.3.2. Random Effects Model:
![]()
which is chi-square distributed with n – 1 degrees of freedom. The weights here are always the inverse variance weights but when the Mantel-Haenszel option is selected, the average is the Mantel-Haenszel average. You can override this and use the inverse variance average for M by entering 1 for Weights: Inverse Variance or Mantel-Haenszel in the intermediate inputs dialogue.
I-square: This is a percentage calculated as:
![]()
where df = n – 1.
Lower values of I2 indicate less heterogeneity. The confidence intervals for I2 are calculated as in Higgins & Thompson (2002).
Tests for Publication Bias
Forest, funnel and precision plots provide a visual guide whether the studies being analysed are biased in positive or negative direction. The following two tests provide a statistical measure for publication bias.
Begg-Mazumdar Rank Correlation: The Kendall’s rank correlation coefficient is calculated (Begg & Mazumdar, 1994) between the standardised effect size differences:
![]()
and the standardised variances of effect sizes:
![]()
where the weights are the inverse variance weights.
Egger Regression: A bivariate linear regression (Egger, Smith, Schneider & Minder, 1997) is run between the standardised effect sizes:
![]()
against their precisions:
![]()
where the weights are the inverse variance weights.
6.8.4.3. Forest Plot
A high-resolution forest plot is drawn with study names on the left Y-axis and on the right Y-axis, the summary effect, its confidence interval and the relative weights.
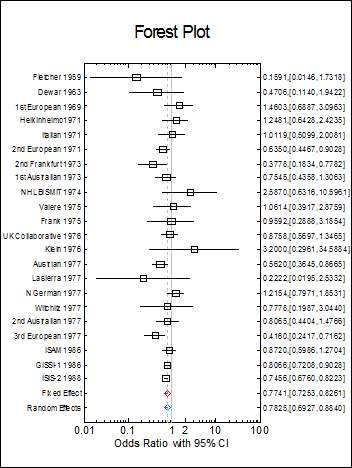
By default, UNISTAT produces a forest plot in landscape orientation. If, however, there are too many studies included in the analysis, you can select Export → Metafile Orientation → Portrait option from the graphics window menu.
Using the Edit → View dialogue, you can choose to display one, none or both fixed and random effects, weights and symbols proportional to the weights. When both fixed and random effects are selected, the fixed weights are displayed. Symbols are not drawn proportional to weights when the weights box is unchecked or the absolute weights are displayed (as opposed to percentage weights).
As in other graphics procedures, X-axis parameters can be changed from the Edit → Scale dialogue. Although Y-axis scale parameters cannot be changed, you can change the font size to accommodate for a large number of studies.
The three different types of symbols displayed in the graph can be changed using the Edit → Lines dialogue.
6.8.4.4. Funnel Plot
Standard error of individual studies are plotted against their effect size. A vertical line is drawn through the summary effect size, which can be fixed or random. Confidence interval is drawn at 95% level by default, but this can be changed by the user.
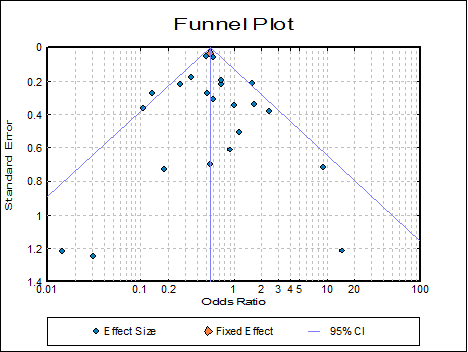
You can edit the lines and symbols and choose to display study names next to each symbol using the Edit → Lines dialogue.
The Summary Effect tab on the same dialogue allows you to display the funnel plot using random effects, instead of the fixed effect.
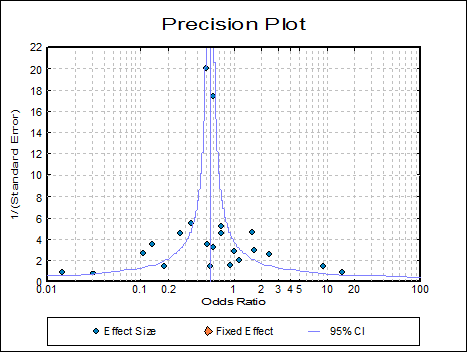
6.8.4.5. Precision Plot
This is similar to funnel plot, but the reciprocal of the individual study standard errors are plotted against their effect sizes.