6.8.2. Input Data Types
UNISTAT classifies commonly used data types into four groups:
1) 2 x 2 Tables
2) Ratios
3) Unpaired Samples
4) Paired Samples
Once the columns of the data matrix to be used in the analysis are selected as [Variable]s in the Variable Selection Dialogue, a second dialogue facilitates assigning a specific input data type and a task to each variable.
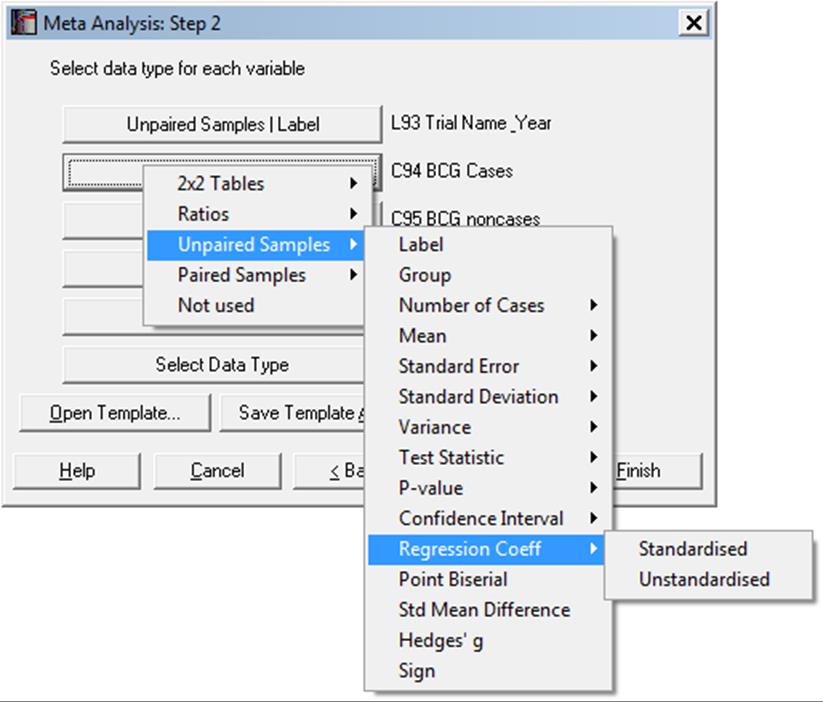
This three-level menu system allows you to combine almost any type of study result entered in a simple spreadsheet format. Once the selections are made, you can save them to a file so that the selection process is not unnecessarily repeated. The default extension for meta analysis template file is .MTA.
The full extent of selection possibilities for these six data groups are given in the following tables.
|
2 x 2 Tables |
Ratios |
Unpaired Samples |
Paired Samples |
|
Label |
Label |
Label |
Label |
|
Group |
Group |
Group |
Group |
|
Cells |
Odds Ratio |
Number of Cases |
Number of Pairs |
|
A |
Odds Ratio |
Cases A |
Mean |
|
B |
Ln(Odds Ratio) |
Cases B |
Mean A |
|
C |
Risk Ratio |
Mean |
Mean B |
|
D |
Risk Ratio |
Mean A |
Mean Diff |
|
Sums |
Ln(Risk Ratio) |
Mean B |
Standard Error |
|
A+B |
Rate Ratio |
Mean Diff |
Std Err A |
|
C+D |
Rate Ratio |
Standard Error |
Std Err B |
|
Ratios |
Ln(Rate Ratio) |
Std Err A |
Std Err Diff |
|
A/(A+B) |
Hazard Ratio |
Std Err B |
Std Err Corr |
|
C/(C+D) |
Hazard Ratio |
Std Err Pooled |
Standard Deviation |
|
Chi-Square |
Ln(Hazard Ratio) |
Std Err Overall |
Std Dev A |
|
Chi-Square |
Risk Difference |
Standard Deviation |
Std Dev B |
|
Number of Cases |
Rate Difference |
Std Dev A |
Std Dev Diff |
|
Sign |
Observed – Expected |
Std Dev B |
Std Dev Corr |
|
Pairs |
Standard Error |
Std Dev Pooled |
Variance |
|
P pair |
Standard Error |
Std Dev Overall |
Var A |
|
Q pair |
Ln(Std Err) |
Variance |
Var B |
|
R pair |
Variance |
Var A |
Var Diff |
|
S pair |
Variance |
Var B |
Var Corr |
|
Rho |
Ln(Variance) |
Var Pooled |
Test Statistic |
|
Confidence Interval |
Var Overall |
t-stat |
|
|
Lower Bound |
Test Statistic |
F-stat |
|
|
Upper Bound |
t-stat |
Z-stat |
|
|
Confidence Level |
F-stat |
P-value |
|
|
Z-stat |
P (t-dist) |
||
|
P-value |
P (F-dist) |
||
|
P (t-dist) |
P (normal) |
||
|
P (F-dist) |
Tails |
||
|
P (normal) |
Confidence Interval |
||
|
Tails |
Lower Bound |
||
|
Confidence Interval |
Upper Bound |
||
|
Lower Bound |
Confidence Level |
||
|
Upper Bound |
Correlation |
||
|
Confidence Level |
Fisher’s Z |
||
|
Regression Coeff |
Std Mean Diff |
||
|
Standardised |
Sign |
||
|
|
|
Unstandardised |
|
|
|
|
Point Biserial Corr |
|
|
|
|
Std Mean Diff |
|
|
|
|
Hedges’ g |
|
|
|
|
Sign |
|
6.8.2.1. 2 x 2 Tables
Normally, cell frequencies from a 2 x 2 table are entered for each study. However, UNISTAT also accepts data in the form of sums and ratios. If one or more cell frequencies are zero, 0.5 is added to all four frequencies. Optionally, if the data is paired, an external correlation ρ (rho) can be entered.
The commonly used effect sizes for 2 x 2 tables are as follows:
Odds ratio:
![]()
![]()
Peto odds ratio:
![]()
where:
![]()
![]()
![]()
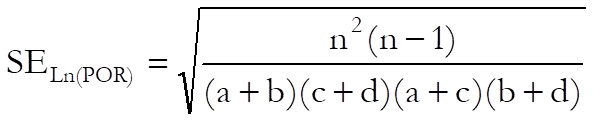
Risk ratio:
![]()
![]()
Risk difference:
![]()
![]()
Standardised mean difference:
![]()
![]()
Correlation from a chi-square statistic and sample size for a 2 x 2 table:
If a chi-square statistic and sample size from a 2 x 2 table is reported by a study, the correlation and its standard error are calculated as:
![]()
![]()
Event pairs:
Define each cell frequency from pairs data as:
A = P + Q
B = P + R
C = R + V
D = Q + V
For the calculation of other effect size measures based on d, see 6.8.2.3. Unpaired Samples.
6.8.2.2. Ratios
Given the odds ratio and its dispersion measure, the standardised mean difference d is calculated as above. Other ratios can only be compared within their own group.
6.8.2.3. Unpaired Samples
Select this option if the individual study is based on unpaired (or unmatched or independent or unequal size) samples consisting of continuous data.
The following data entry combinations are possible to calculate the standardised mean difference d, which is one of the most commonly used summary effect size for continuous data.
Sample sizes and means are given:
When the standard deviations are given, the standardised mean difference is calculated as:
![]()
where sp is the pooled standard deviation:
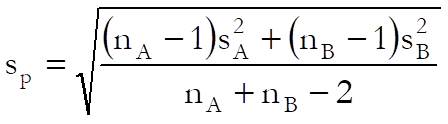
The standard error of d is calculated as:
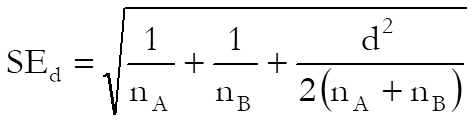
When standard errors or variances are given for samples A and B, standard deviations are calculated first.
UNISTAT also accepts data where difference in means is given instead of individual means and pooled or overall standard deviation is given instead of individual standard deviations.
When the overall standard deviation is given, the pooled standard deviation is calculated as:
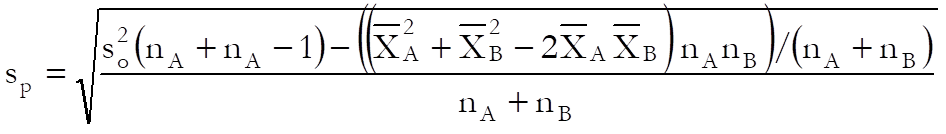
The overall standard error and variance are converted into overall standard deviation first.
Sample sizes and the test statistic are given:
t-statistic is given:
![]()
The standard error of d is calculated as above.
F-statistic from a one-way ANOVA is given:
Find t-statistic as:
![]()
and use the formula for t-statistic to calculate the standardised mean difference.
Z-statistic is given:
The Z-statistics can be used instead of t-statistic:
![]()
and the formula for t-statistic is used to calculate the standardised mean difference.
Sample sizes and the p-value are given:
P-value from a t-test and its tail (1 or 2) are given: The t-value is found using the inverse t-distribution with nA + nB – 2 degrees of freedom. If the tail value is not specified, a two-tailed test is assumed.
P-value from an F-test is given: The F-value is found using the inverse F-distribution with 1 and nA + nB – 2 degrees of freedom.
P-value from a Z-test and its tail (1 or 2) are given: The Z-value is found using the inverse normal distribution. If the tail value is not specified, a two-tailed test is assumed.
Standardised regression coefficient:
Enter the standard deviation of dependent variable as Sample B standard deviation (or standard error or variance).
![]()
where b is the standardised regression coefficient and the pooled standard deviation is calculated as:
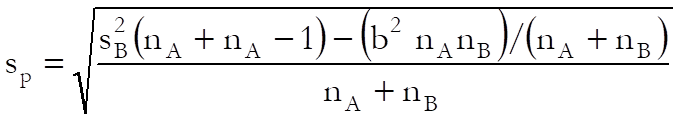
The standard error of d is calculated as in the Sample sizes and means are given option above.
Unstandardised regression coefficient:
Enter the standard deviation of dependent variable as Sample B standard deviation (or standard error or variance). Standard deviation of sample A (which is assumed to be a binary variable containing 0s and 1s only) is calculated as:
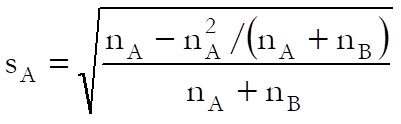
Given the unstandardised regression coefficient β, the standardised regression coefficient b and d are calculated as:
![]()
![]()
where the pooled standard deviation is as calculated as above. The standard error of d is calculated as in the Sample sizes and means are given option above.
Point Biserial Correlation:
![]()
where:
![]()
The standard error of d is calculated as in the Sample sizes and means are given option above. If a p-value is given for point biserial correlation, select the P-value from a t-test option above.
Other effect sizes based on standardised mean difference are calculated as follows.
Mean Difference:
![]()
and its standard error is:
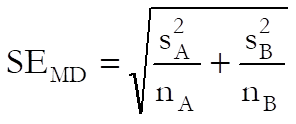
Hedges’ g:
Hedges’ correction factor for standardised mean difference d is:
![]()
where:
![]()
Hedges’ g is defined as:
![]()
The standard error of Hedges’ g can be calculated in one of the two following ways, which can be selected from the intermediate inputs dialogue. The default and recommended SE is:
![]()
and the alternative definition is:
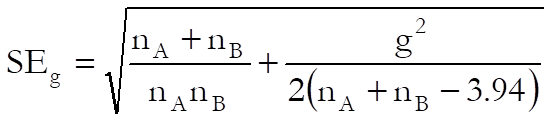
Odds Ratio:
The correction factor for log odds ratio is:
![]()
The log odds ratio and its standard error can be calculated from standardised mean difference as:
![]()
![]()
The odds ratio is:
![]()
Correlation:
Given standardised mean difference and its standard error, the correlation and its SE are calculated as:
![]()
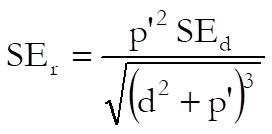
where:
![]()
and:
![]()
Fisher’s Z:
Fisher’s Z and its standard error are calculated from a given correlation as:
![]()
![]()
6.8.2.4. Paired Samples
This option should be selected when the individual study is based on paired (or matched or equal size) samples consisting of continuous data. This group also includes correlation coefficients and pre/post correlations. If the correlation value is not available, the imputed r value is used instead. The default value for imputed r is 0.5.
When only a t-statistic and the sample size are given, there are two ways of calculating the effect size. If the t-statistic was originally reported for a correlation coefficient, then in the intermediate inputs dialogue choose Yes for Use paired t-test box.
The following data entry combinations are possible to calculate the standardised mean difference d. Other effect sizes based on standardised mean difference are calculated as in unpaired samples above.
Sample size, means and standard deviations are given:
The standardised mean difference is calculated as:
![]()
where:
![]()
When r is not available and it is substituted by the imputed r value of 0.5, the correction factor for the correlation (i.e. the term in square brackets) simply disappears and the standardised mean difference formula becomes identical to the unpaired samples case.
The standard error of d is calculated as:
![]()
When standard error or variance is given for the paired differences, standard deviations are calculated first.
UNISTAT also accepts mean difference and standard deviation instead of individual means and standard deviations.
Sample size and the test statistic are given:
t-statistic is given:
![]()
The standard error of d is calculated as above.
F-statistic from a one-way ANOVA is given:
Find t-statistic as:
![]()
and use the above formula to find d.
Z statistic is given:
![]()
Sample size and the test statistic are given (paired t-test):
To use paired t-test for correlations you need to select this option from the intermediate inputs dialogue first. The correlation is calculated as:
![]()
![]()
The standard error of d is calculated as.
![]()
where:
![]()
Sample sizes and p-values are given:
P-value from a t-test and its tail (1 or 2) are given: The t-value is found using the inverse t-distribution with nA + nB – 2 degrees of freedom. If the tail value is not specified, a two-tailed test is assumed.
P-value from an F-test is given: The F-value is found using the inverse F-distribution with 1 and nA + nB – 2 degrees of freedom.
P-value from a Z-statistic and its tail (1 or 2) are given: The Z-value is found using the inverse normal distribution. If the tail value is not specified, a two-tailed test is assumed.
