7.4.5. Heterogeneity of Regression
This procedure (which is also known as analysis of covariance) is used to test whether slopes and / or intercepts of a number of bivariate regression lines are significantly different. These are also known as slope or parallelism tests. Data in two different formats can be analysed:
1) Data is in One or More Columns: Select an [X-Axis] variable and any number of Y-Axis variables by clicking [Variable]. Each Y-Axis variable is regressed against the same X-Axis variable.
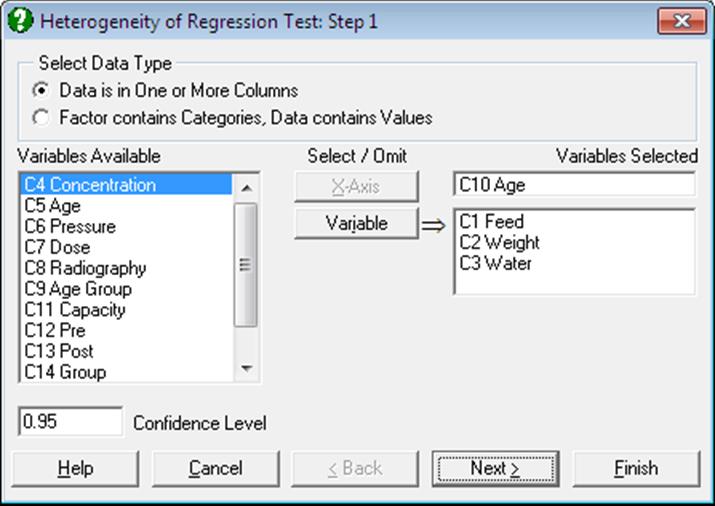
2) Factor contains Categories, Data contains Values: Select a [Data] column and a [Factor] column: Subgroups of [Data] defined by the levels of [Factor] are the Y-Axis variables. You are also required to select an [X-Axis] variable which has the same length as the other two. In this case it is possible to regress each Y-Axis variable against different values of the [X-Axis] variable.
7.4.5.1. Heterogeneity of Regression Test Results
regression, as well as the pooled, common and total regressions. For the pooled regression, the residual SS and residual DF are the sums of individual SS and DF values respectively. For the common regression, sum of all individual difference sum of squares are used to compute the residual SS figure. The residual DF is the total number of cases minus number of regressions minus one. For the total regression all Y-Axis variables are regressed on the X-Axis variable. Three null hypotheses are tested:1) All slopes are equal:
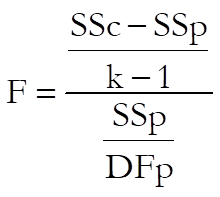
with k - 1 and DFp degrees of freedom.
2) All intercepts are equal:
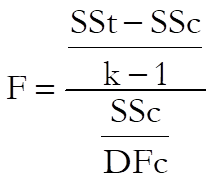
with k - 1 and DFc degrees of freedom. This test statistic can also be obtained by running an analysis of covariance where X-Axis variable is the covariate, Y-Axis variable is the data, and the factor is the classification variable. The F-statistic on the main effect and its probability are identical to the results obtained using the present method.
3) All regressions are equal:
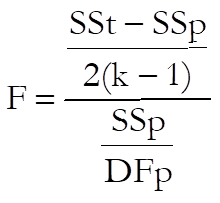
with 2(k - 1) and DFp degrees of freedom.
7.4.5.2. Heterogeneity of Regression Multiple Comparisons
If one of the three null hypotheses is rejected then multiple comparison tests can be performed to find out which slopes or intercepts are significantly different. Here we provide a Tukey-HSD type test to compare all possible pairs of regressions for their slopes and / or intercepts and a Dunnett type test to compare all regression lines against a control line.
Note that multiple comparison of intercepts is only meaningful when the equality of slopes is accepted. Accordingly, when the differences between intercepts are calculated, the slopes of individual lines are all assumed to be equal to the slope of the common regression. Therefore, the values of the difference column in the comparison table do not necessarily correspond to differences between actual intercepts (see Zar (2010), p. 376, equation 18.39).
7.4.5.3. Heterogeneity of Regression Examples
Example 1
Examples 9.3 on p. 295, p. 300 and 9.4. on p. 304 in Armitage, P. & G. Berry (1994). Ages and vital capacities for three groups of workers in the cadmium industry are given, where x is the age last birthday (years) and y is vital capacity (litres).
The data in Table 9.4. is given in the form of pairs of columns, one for x and one for y in different groups. In order to analyse this data in UNISTAT, all x values should be stacked in one column, y values in another column and a third column (Group) should be created to keep track of group memberships. Therefore, the resulting data matrix should have 84 rows and 3 columns.
Open ANOTESTS and select Statistics 1 → Tests for ANOVA → Heterogeneity of Regression. From the Variable Selection Dialogue select the second data option Factor contains categories Data contains values, assign Age Group (C9) as [Factor], Age (C10) as [X-Axis] and Capacity (C11) as [Data]. The following results are obtained:
Heterogeneity of Regression Test
Test Results
X Axis: Age, Dependent Variable: Capacity, classified by Age Group
|
Regression |
Cases |
Intercept |
Slope |
Residual SS |
R-DF |
|
1 |
12 |
8.1834 |
-0.0851 |
5.1311 |
10 |
|
2 |
28 |
6.2300 |
-0.0465 |
7.6050 |
26 |
|
3 |
44 |
5.6803 |
-0.0306 |
14.7991 |
42 |
|
Pooled |
* |
* |
* |
27.5352 |
78 |
|
Common |
84 |
6.0048 |
-0.0398 |
30.0347 |
80 |
|
Total |
84 |
6.0333 |
-0.0405 |
30.1964 |
82 |
|
Null hypothesis: All slopes are equal |
|
|
F(2,78) = |
3.5402 |
|
Right-Tail Probability = |
0.0338 |
|
Null hypothesis: All intercepts are equal |
|
|
F(2,80) = |
0.2153 |
|
Right-Tail Probability = |
0.8067 |
|
Null hypothesis: All regressions are identical |
|
|
F(4,78) = |
1.8846 |
|
Right-Tail Probability = |
0.1215 |
Note that the total regression results given by Armitage & Berry on p. 300 correspond to common regression results above. According to the approach adopted here (following Zar (2010), pp. 375-378) the total regression is identical to the one run on all groups. This discrepancy does not affect the test of slopes, but it does affect the tests of intercepts and regressions.
Since the between slopes F‑value of 3.54 has a tail probability less than 5% then reject the first null hypothesis that “slopes are the same”. It cannot be rejected at a 99% confidence level. The between groups F‑value of 0.22 has a tail probability of 0.81, then do not reject the second null hypothesis that “the intercepts are the same”. Multiple comparisons will answer the question which slopes are different.
Multiple comparisons for slopes
Method: 95% Tukey-HSD interval.
** denotes significantly different pairs.
A pairwise test result is significant if its q stat value is greater than the table q.
|
Group |
SSQ(x) |
Slope |
1 |
2 |
3 |
|
|
1 |
912.2500 |
-0.0851 |
|
|
** |
| |
|
2 |
2282.7143 |
-0.0465 |
|
|
|
|| |
|
3 |
6197.1591 |
-0.0306 |
** |
|
|
| |
|
Comparison |
Difference |
Standard Error |
q Stat |
Table q |
Probability |
|
3 - 1 |
0.0545 |
0.0146 |
3.7276 |
3.3765 |
0.0269 |
|
2 - 1 |
0.0386 |
0.0161 |
2.3890 |
3.3765 |
0.2155 |
|
3 - 2 |
0.0159 |
0.0101 |
1.5771 |
3.3765 |
0.5075 |
|
Comparison |
Lower 95% |
Upper 95% |
Result |
|
3 - 1 |
0.0051 |
0.1039 |
** |
|
2 - 1 |
-0.0159 |
0.0931 |
|
|
3 - 2 |
-0.0182 |
0.0500 |
|
Multiple comparisons for intercepts
Method: 95% Tukey-HSD interval.
** denotes significantly different pairs.
A pairwise test result is significant if its q stat value is greater than the table q.
|
Group |
Cases |
Intercept |
1 |
2 |
3 |
|
|
1 |
12 |
5.9630 |
|
|
|
| |
|
2 |
28 |
6.0013 |
|
|
|
| |
|
3 |
44 |
6.0729 |
|
|
|
| |
|
Comparison |
Difference |
Standard Error |
q Stat |
Table q |
Probability |
|
3 - 1 |
0.1099 |
0.1428 |
0.7698 |
3.3765 |
0.8497 |
|
2 - 1 |
0.0383 |
0.1669 |
0.2297 |
3.3765 |
0.9856 |
|
3 - 2 |
0.0716 |
0.1001 |
0.7156 |
3.3765 |
0.8686 |
|
Comparison |
Lower 95% |
Upper 95% |
Result |
|
3 - 1 |
-0.3723 |
0.5922 |
|
|
2 - 1 |
-0.5252 |
0.6018 |
|
|
3 - 2 |
-0.2663 |
0.4095 |
|
Multiple comparisons for slopes
Method: 95% Dunnett interval.
Control Group: 1, Two-Tailed Test
** denotes significantly different pairs.
A pairwise test result is significant if its q stat value is greater than the table q.
|
Group |
SSQ(x) |
Slope |
1 |
|
|
1 |
912.2500 |
-0.0851 |
|
| |
|
2 |
2282.7143 |
-0.0465 |
|
| |
|
3 |
6197.1591 |
-0.0306 |
** |
| |
|
Comparison |
Difference |
Standard Error |
q Stat |
Table q |
Probability |
|
3 - 1 |
0.0545 |
0.0207 |
2.6358 |
2.1922 |
0.0168 |
|
2 - 1 |
0.0386 |
0.0228 |
1.6893 |
2.1922 |
0.1442 |
|
Comparison |
Lower 95% |
Upper 95% |
Result |
|
3 - 1 |
0.0092 |
0.0998 |
** |
|
2 - 1 |
-0.0115 |
0.0886 |
|
Multiple comparisons for intercepts
Method: 95% Dunnett interval.
Control Group: 1, Two-Tailed Test
** denotes significantly different pairs.
A pairwise test result is significant if its q stat value is greater than the table q.
|
Group |
Cases |
Intercept |
1 |
|
|
1 |
12 |
5.9630 |
|
| |
|
2 |
28 |
6.0013 |
|
| |
|
3 |
44 |
6.0729 |
|
| |
|
Comparison |
Difference |
Standard Error |
q Stat |
Table q |
Probability |
|
3 - 1 |
0.1099 |
0.2020 |
0.5443 |
2.2066 |
0.7704 |
|
2 - 1 |
0.0383 |
0.2360 |
0.1624 |
2.2066 |
0.9755 |
|
Comparison |
Lower 95% |
Upper 95% |
Result |
|
3 - 1 |
-0.3357 |
0.5556 |
|
|
2 - 1 |
-0.4825 |
0.5591 |
|
Example 2
Table 8.1 on p. 326 from Tabachnick, B. G. & L. S. Fidell (1989). A reading test is given to disabled children before and after an experiment where two different teaching methods are applied to two thirds of children and one third are kept as controls. We would like to find out whether the teaching methods have significant effects on test results, having made an adjustment for their pre-test reading abilities.
The table format given in the book can be transformed into the factor format by using UNISTAT’s Data → Stack Columns procedure and the Level() function (see 3.4.2.5. Statistical Functions). All Pre and Post data should be stacked in two columns and a factor column Group created to keep track of the group memberships. Therefore, the resulting data matrix should have 9 rows and 3 columns.
Open ANOTESTS and select Statistics 1 → Tests for ANOVA → Heterogeneity of Regression. From the Variable Selection Dialogue select the second data option Factor contains categories Data contains values, assign Group (C14) as [Factor], Pre (C12) as [X-Axis] and Post (C13) as [Data]. Selecting only the Test Results output option the following results are obtained:
Heterogeneity of Regression Test
X Axis: Pre, Dependent Variable: Post, classified by Group
|
Regression |
cases |
Intercept |
Slope |
Residual SS |
R-DF |
|
1 |
3 |
50.3073 |
0.5917 |
0.5550 |
1 |
|
2 |
3 |
22.8759 |
0.8759 |
60.6353 |
1 |
|
3 |
3 |
19.1923 |
0.7821 |
84.9615 |
1 |
|
Pooled |
***** |
***** |
***** |
146.1519 |
3 |
|
Common |
9 |
30.0816 |
0.7591 |
149.4387 |
5 |
|
Total |
9 |
17.6851 |
0.9030 |
515.6399 |
7 |
|
Null hypothesis: All slopes are equal |
|
|
F(2,3) = |
0.0337 |
|
Right-Tail Probability = |
0.9672 |
|
Null hypothesis: All intercepts are equal |
|
|
F(2,5) = |
6.1263 |
|
Right-Tail Probability = |
0.0452 |
|
Null hypothesis: All regressions are identical |
|
|
F(4,3) = |
1.8961 |
|
Right-Tail Probability = |
0.3131 |
Although the null hypotheses “all slopes are equal” is not rejected, “all intercepts are equal” (that the different teaching methods do not have significant effects) should be rejected (since 0.0452 < 0.05).