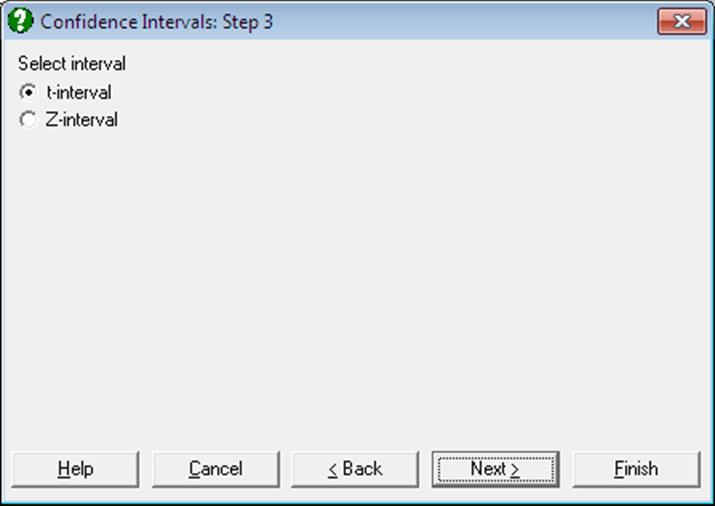
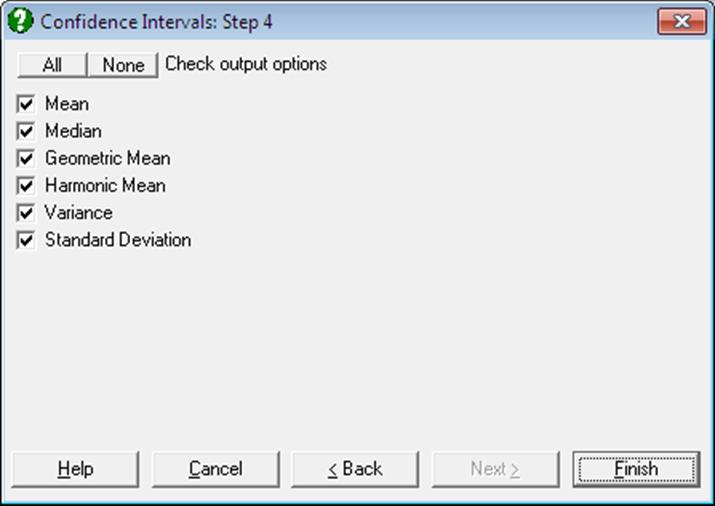
5.1.2. Confidence Intervals

Confidence intervals for mean, median, geometric and harmonic means (t- or Z‑intervals) and intervals for variance and standard deviation can be computed. Data input is in multisample format (see 5.0.1. Multisample Data Types).

By default, intervals for means are based on the t-distribution with a critical value of . It is possible to calculate intervals using the standard normal distribution with a critical value of . The confidence level 1 - α can be defined in Variable Selection Dialogue.

Mean:

     

     

Median: The methods used in computing the median and its confidence limits are reported in the header. These methods can be changed using the dialogues of the Quantiles (Percentiles) procedure (see sections 5.1.3.1. Quantile Methods and 5.1.3.2. Quantile Interval Methods).

Geometric Mean: Assuming Ln(X_i) i = 1,…, n are normally distributed, the limits are defined as:

     

     

      where G is the geometric mean and the term a_G (which is not the standard error of geometric mean) is defined as:

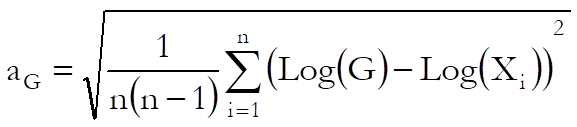
Harmonic Mean: Assuming 1/X_i i = 1,…, n are normally distributed, the confidence interval is:

     

     

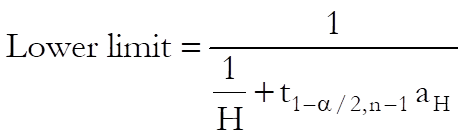
      where H is the harmonic mean and the term a_H (which is not the standard error of harmonic mean) is defined as:

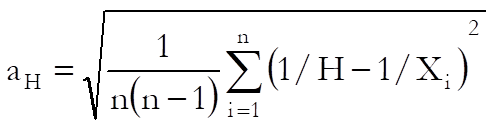
Variance: The 100(1 - α)% confidence interval for the variance is constructed using the chi-square distribution with n – 1 degrees of freedom:

     

     

      where s² is the sample variance.

Standard Deviation: The lower and upper limits are the square roots of corresponding limits for variance.

Example

Open ANOVA and select Statistics 1 → Descriptive Statistics → Confidence Intervals and from the Variable Selection Dialogue select AUC (C20) as [Variable] and Treatment (S19) as [Factor] and click [Finish].

Confidence Intervals

Data variable: AUC

Subsample selected by: Treatment = A

Number of Cases: 12

 

	Value	Lower 95%	Upper 95%
* Mean	209.4167	169.1754	249.6580
** Median	200.5000	154.0000	290.0000
* Geometric Mean	199.8379	161.9368	246.6098
* Harmonic Mean	189.4269	153.3584	247.6786
Variance	4011.3561	2012.9935	11563.8961
Standard Deviation	63.3353	44.8664	107.5356

* t-interval

** Quantile Method: Simple Average, Interval Method: Normal Approximation

 

Data variable: AUC

Subsample selected by: Treatment = B

Number of Cases: 12

 

	Value	Lower 95%	Upper 95%
* Mean	167.1667	137.7396	196.5937
** Median	165.5000	133.0000	210.0000
* Geometric Mean	160.4173	131.3584	195.9047
* Harmonic Mean	152.6247	123.7428	199.0937
Variance	2145.0606	1076.4422	6183.7587
Standard Deviation	46.3148	32.8092	78.6369

* t-interval

** Quantile Method: Simple Average, Interval Method: Normal Approximation

Go back to the Variable Selection Dialogue omit Treatment (S19) from the [Factor] list and select the Z interval option on the next dialogue.

Confidence Intervals

Data variable: AUC

Number of Cases: 24

 

	Value	Lower 95%	Upper 95%
* Mean	188.2917	164.9290	211.6543
** Median	187.5000	154.0000	220.0000
* Geometric Mean	179.0460	156.5802	204.7352
* Harmonic Mean	169.0460	146.8020	199.2349
Variance	3410.0417	2059.8730	6710.0662
Standard Deviation	58.3956	45.3858	81.9150

* Z-interval

** Quantile Method: Simple Average, Interval Method: Normal Approximation