10.1. Parallel Line Method

Balanced, symmetric or unbalanced assays can be analysed. The analysis is based on a regression of the response variable against the natural logarithm of the dose variable. A separate line is fitted on each preparation, subject to a constraint that they should be parallel. An assay is said to be balanced when:

1)    there is an equal number of cases in each treatment group,

2)    there is an equal number of dose groups for each preparation and

3)    successive dose levels are the same for all preparations.

An assay fulfilling the first two conditions but having different dose levels for different preparations (yet having the same ratio of successive dose levels) will be called symmetric. Assays not fulfilling one or more of these conditions will be called asymmetric or unbalanced.

For validity tests, the following Analysis of Variance (ANOVA) options are available:

1)    Completely randomised design

2)    Randomised block design

3)    Latin square design

4)    Twin and triple crossover designs

The unbalanced assays can only be analysed using the Completely Randomised Design option. All other options require symmetric or balanced assays. In most cases, the program will detect whether an assay is unbalanced, symmetric or balanced and apply the relevant algorithm automatically.

Note that the example data sets given in European Pharmacopoeia (1997-2017) Parallel Line Method are all balanced.

10.1.1. Parallel Line Variable Selection

Once the data is arranged as described above (see section 10.0.1. Data Preparation), select Bioassay → Parallel Line Method from UNISTAT menus. A Variable Selection Dialogue will pop up.

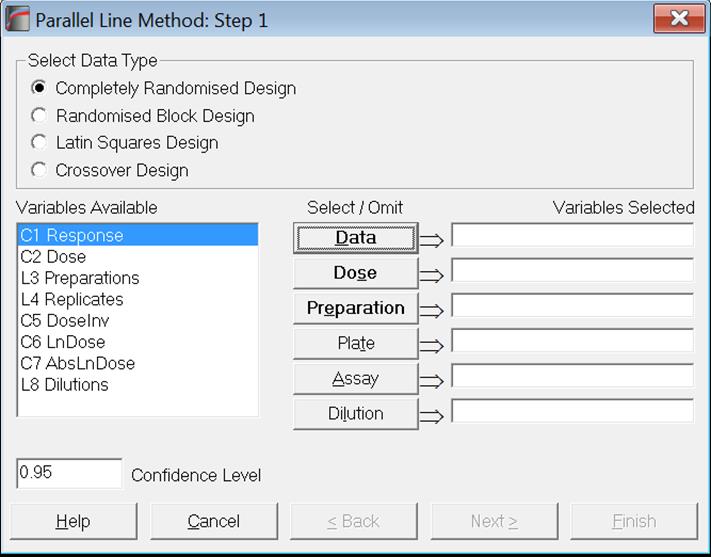
Data columns available for selection are listed on the left. Variables are referred to by their column numbers, which are prefixed by a single letter representing the type of data. For instance, in the above example C1, C2 and C4 are numeric columns, whereas L3 means that column three contains Long Strings. Columns containing Short Strings (up to 8 characters) are prefixed by (S). Other data types that will probably not be used in bioassays are date (D) and time (T). If Column Labels have been entered, they will also appear in the list next to the column numbers.

You will need to assign tasks to variables by sending them to boxes on the right. To do this, highlight the variable on the left list and click on the desired task button (i.e. one of the command buttons in the middle of the dialogue). Likewise, you can deselect an already selected variable by highlighting it on the right list first and then clicking its task button.

Designs can be unbalanced, i.e. the number of replicates for each dose-preparation combination may be different, dose levels for standard and test preparations may be different, there can be more than one test preparation, but the first five characters of the standard preparation label should be “stand” or “refer” in any language (capitalisation is not significant). Otherwise the first preparation encountered in the [Preparation] column will be considered as the standard. It is compulsory to select at least three variables [Data], [Dose] and [Preparation], which have bold button fonts. There are three optional variables [Plate], [Assay] and [Dilution]. A plate effect, that will be subtracted from the residual sum of squares, can be calculated if required. For the latter two options see sections 10.0.4. Multiple Assays with Combination and 10.0.2. Doses, Dilutions and Potency respectively. Note that if the design is balanced, the plate effect will generate the same results as Randomised Block Design.

The frame Select Data Type (at the top) displays options for the type of Analysis of Variance to be performed. The number of variables to be selected is different for these types of analyses. When the second option Randomised Block Design is selected, four compulsory variables will need to be selected.

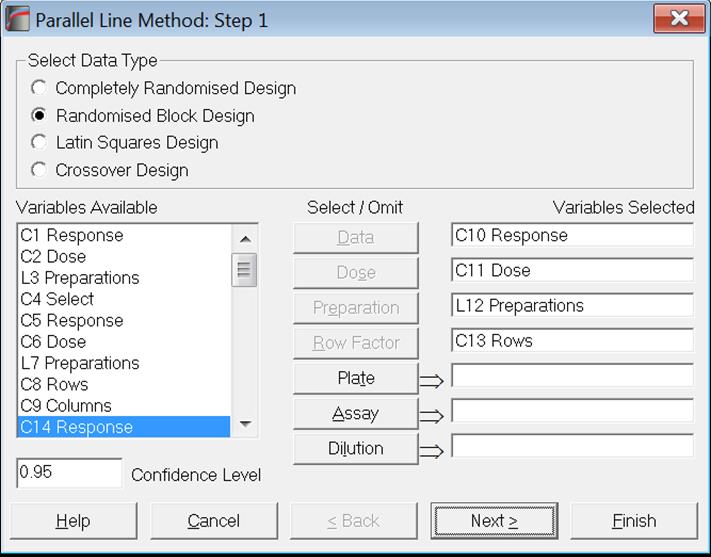
The third and fourth options Latin Square Design and Crossover Design require selection of five variables.

When all variables are selected, click the [Next] button to proceed to Output Options Dialogue.

10.1.2. Parallel Line Output Options

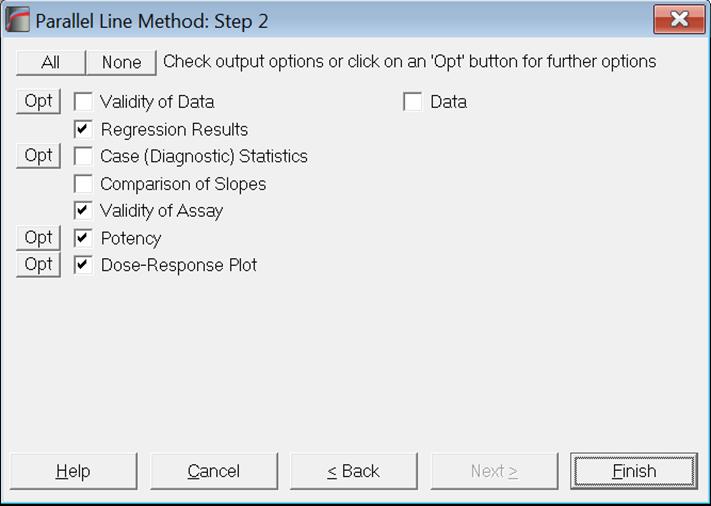
Output options that have further options under them (i.e. further dialogues and windows to display) have an [Opt] button placed to the left of their check boxes. When you click [Finish] without clicking on an [Opt] button first, the program will generate output with default selections. If you want to change the defaults, you can click on the [Opt] button to display further dialogues for this particular output option. Then you can either obtain this particular output option on its own by clicking [Finish], or click [Back] to display the Output Options Dialogue again and output all selected options together.

Data

This output option (which is available for all bioassay analysis methods supported here) will enable the user to include a printout of data used in the analysis as part of the output. This will be useful in fulfilling reporting and data integrity requirements.

Data

	Response	Dose	Preparations
1	161	1	Standard S
2	151	1	Preparation T
3	162	1.5	Preparation T
4	194	2.25	Standard S
5	176	1.5	Standard S
6	193	2.25	Preparation T
7	160	1	Preparation T
8	192	2.25	Preparation T
9	195	2.25	Standard S
10	184	1.5	Standard S
11	181	1.5	Preparation T
12	166	1	Standard S
13	178	1.5	Preparation T
14	150	1	Standard S
15	174	1.5	Standard S
16	199	2.25	Preparation T
17	201	2.25	Standard S
18	161	1	Preparation T
19	187	2.25	Standard S
20	172	1.5	Standard S
21	161	1	Standard S
22	160	1	Preparation T
23	202	2.25	Preparation T
24	186	1.5	Preparation T
25	171	1.5	Standard S
26	170	1.5	Preparation T
27	193	2.25	Preparation T
28	163	1	Standard S
29	154	1	Preparation T
30	198	2.25	Standard S
31	194	2.25	Preparation T
32	192	2.25	Standard S
33	151	1	Preparation T
34	171	1.5	Preparation T
35	151	1	Standard S
36	182	1.5	Standard S

 

10.1.2.1. Validity of Data

One of the basic assumptions of Parallel Line Method is that for each treatment group (i.e. a unique dose-preparation combination) observations are normally distributed. Normality, homogeneity of variance and outliers of treatment groups can be detected and tested using the following descriptive statistics, tests and plotting procedures provided under this comprehensive menu option.

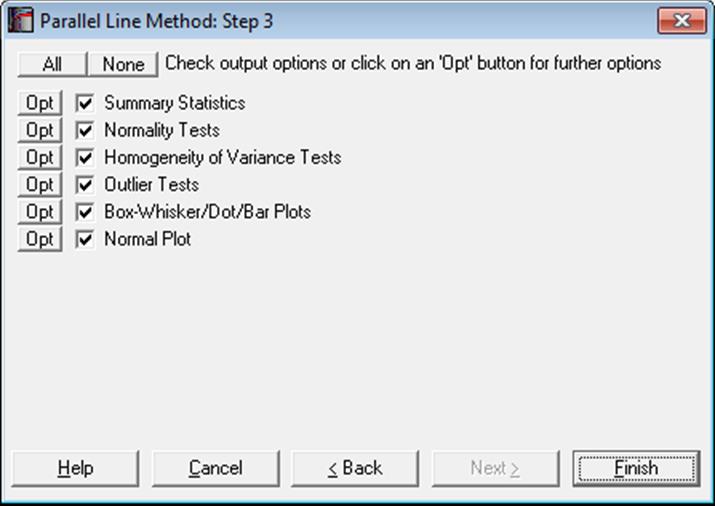
Note that under each test type we provide multiple alternatives. There are four normality tests, five homogeneity of variance tests and three outlier tests. In most cases you will need to use only one of these tests from each type. You can simply uncheck the tests you do not need and UNISTAT will remember your choices in future session.

10.1.2.1.1. Summary Statistics

The selected statistics will be displayed for each unique dose-preparation group.

For more information see section 5.1.1. Summary Statistics.

Example

Summary Statistics

Data variable: Response

Subsample selected by: Dose x Preparations

Quantile Method: Simple Average

	Valid Cases	Mean	Median	Variance
1 x Standard S	6	158.6667	161.0000	43.4667
1 x Preparation T	6	156.1667	157.0000	22.1667
1.5 x Standard S	6	176.5000	175.0000	28.7000
1.5 x Preparation T	6	174.6667	174.5000	75.0667
2.25 x Standard S	6	194.5000	194.5000	23.5000
2.25 x Preparation T	6	195.5000	193.5000	16.3000

 

10.1.2.1.2. Normality Tests

Royston (1995) revision of Shapiro-Wilk normality test is computed as recommended by European Pharmacopoeia (1997-2017). UNISTAT also offers more powerful normality tests such as Cramer-von Mises and Anderson-Darling.  

Pass/Fail test results will be displayed by comparing the calculated p-value to the alpha value provided in the above dialogue. Smaller p-values indicate non-normality.

For more information see section 6.3.3. Normality Tests.

Example

Shapiro-Wilk Normality Test

Alpha = 0.05

Dose x Preparations	Test Statistic	Probability	Pass/Fail
1 x Standard S	0.8581	0.1827	Pass
1 x Preparation T	0.8118	0.0749	Pass
1.5 x Standard S	0.8965	0.3536	Pass
1.5 x Preparation T	0.9757	0.9284	Pass
2.25 x Standard S	0.9879	0.9835	Pass
2.25 x Preparation T	0.8255	0.0984	Pass

 

Kolmogorov-Smirnov Normality Test

Alpha = 0.05

* Lilliefors probability = 0.2 means 0.2 or greater.

Dose x Preparations	Test Statistic	* Probability	Pass/Fail
1 x Standard S	0.3050	0.0851	Pass
1 x Preparation T	0.2922	0.1177	Pass
1.5 x Standard S	0.2038	0.2000	Pass
1.5 x Preparation T	0.1639	0.2000	Pass
2.25 x Standard S	0.1364	0.2000	Pass
2.25 x Preparation T	0.3115	0.0703	Pass

 

Cramer-von Mises Normality Test

Alpha = 0.05

Dose x Preparations	Test Statistic	Probability	Pass/Fail
1 x Standard S	0.0849	0.1450	Pass
1 x Preparation T	0.0886	0.1276	Pass
1.5 x Standard S	0.0544	0.3902	Pass
1.5 x Preparation T	0.0274	0.8514	Pass
2.25 x Standard S	0.0210	0.9388	Pass
2.25 x Preparation T	0.1046	0.0740	Pass

 

Anderson-Darling Normality Test

Alpha = 0.05

Dose x Preparations	Test Statistic	Probability	Pass/Fail
1 x Standard S	0.4756	0.1438	Pass
1 x Preparation T	0.5470	0.0901	Pass
1.5 x Standard S	0.3341	0.3689	Pass
1.5 x Preparation T	0.1760	0.8637	Pass
2.25 x Standard S	0.1514	0.9165	Pass
2.25 x Preparation T	0.5613	0.0818	Pass

 

10.1.2.1.3. Homogeneity of Variance Tests

Another basic assumption of Parallel Line Method is that variances for different treatment groups are not significantly different from each other.

Earlier versions of UNISTAT featured Bartlett’s chi-square test as recommended by European Pharmacopoeia (1997-2017), and Hartley’s F test. Here we provide three more homogeneity of variance tests. The computationally demanding Levene’s test is considered to be more powerful than other homogeneity of variance tests.

Test results are displayed as either Pass or Fail, by comparing the calculated p-value to the alpha value provided in the above dialogue. Smaller p-values indicate non-homogeneity.

For a detailed description of these tests see 7.4.2.1. Homogeneity of Variance Test Results.

Example

Homogeneity of Variance Tests

For 6 groups defined by Dose x Preparations.

Alpha = 0.05

	Test Statistic	Probability	Pass/Fail
Bartlett’s Chi-square Test	3.7817	0.5813	Pass
Bartlett-Box F Test	0.7637	0.5760	Pass
Cochran’s C (max var / sum var)	0.3588	0.2313	Pass
Hartley’s F (max var / min var)	4.6053	0.0500	Pass
Levene’s F Test	1.5818	0.1954	Pass

Hartley’s F probability = 0.05 means 0.05 or greater.

 

10.1.2.1.4. Outlier Tests

For more information see section 6.3.4. Outlier Tests.

In addition to the tests provided here outliers can also be detected using standardised residuals. See section 10.0.6. Outlier Detection, Omission and Replacement.

10.1.2.1.5. Box-Whisker, Dot and Bar Plots

This procedure combines boxplot with dot and error bar plots.

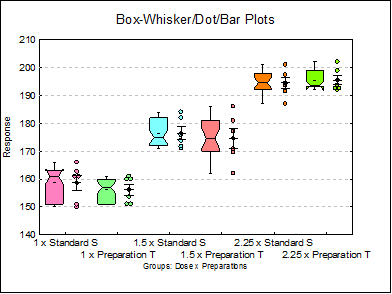
Although all three plot types are displayed on the same graph by default, the user can change graph settings to display any combination of the three plot types, as well as changing other characteristics of the graph. To do this click on the [Opt] button situated to the left of this output option and from the Graphics Editor menu select Edit → Width / Notch / Dots.

For more information see section 5.3.1. Box-Whisker, Dot and Bar Plots.

10.1.2.1.6. Normality Plots

By default all treatments are drawn with a line of best fit on a graph with a probit scale Y-axis against the response on a linear X-axis. If the data lies on a near-straight line, then it is said to conform to the normal distribution.

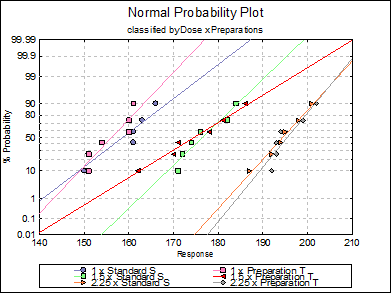
All aspects of the graph can be edited an customised by clicking on the [Opt] button situated to the left of this output option. This will display the Graphics Editor. From the menu select Edit → Data Series.

For more information see sections 6.3.3.5. Normality Plots and 5.3.2. Normal Probability Plot.

10.1.2.2. Regression Results

A separate regression line is fitted on each preparation against the natural logarithm of dose. It is also possible to take logs based 10 by entering the following line:

   LogBase10=1

under the [Bioassay] section of this file:

C:\ProgramData\Unistat\Unistat10\Unistat10.ini

in which case only the slope of regression value will be affected in the output.

The Common Regression is obtained by pooling difference sum of squares for each preparation and regressing the response variable on the log of dose variable. As result, the lines fitted for all preparations will be parallel to each other. The slope of Common Regression is used as the common slope in Potency calculations. Different intercept values indicate different potencies of preparations.

The Pass/Fail test results for R-squared values are optional. The test is performed against a default threshold value of 0.95, which can be changed by the user. For details see section 10.0.5.1. Compliance Output.

Example

Separate Regression

	Intercept	Slope	Residual SS	R-squared	Pass/Fail
Standard S	248.5800	-113.0060	1897.7400	0.9651	Pass
Preparation T	238.5000	-109.5039	747.8000	0.9851	Pass

 

Common Regression

	Intercept	Slope	Residual SS	R-squared	Pass/Fail
Standard S	247.5150	-111.2549	2670.7450	0.9744	Pass
Preparation T	239.5650

 

Residual Variance =	72.1823
Degrees of Freedom =	37

 

10.1.2.3. Case (Diagnostic) Statistics

Estimated Response values (fitted values), residuals and standardised residuals are presented in a table alongside observed responses, doses and preparations.

Model-based outlier detection: Standardised residuals can be used to detect observations that do not fit the data. By their definition, standardised residuals are already in standard deviation units so that a value of 2 means that observation is exactly 2 standard deviations away from the value estimated by the model (Estimated Response). One can therefore determine outliers by setting a threshold, say 2 or 3 (meaning 2 or 3 standard deviations), in which case any observation with a standardised residual greater than 2 or 3 would be reported as an outlier. See section 10.0.6. Outlier Detection, Omission and Replacement.

Example

Case (Diagnostic) Statistics

	Response	Dose	Preparations	Estimated Response	Residuals	Standardised Residuals
1	161	1	Standard S	157.7639	3.2361	0.5684
2	151	1	Preparation T	156.6528	-5.6528	-0.9928
** 3	162	1.5	Preparation T	175.4444	-13.4444	-2.3612
4	194	2.25	Standard S	195.3472	-1.3472	-0.2366
5	176	1.5	Standard S	176.5556	-0.5556	-0.0976
6	193	2.25	Preparation T	194.2361	-1.2361	-0.2171
7	160	1	Preparation T	156.6528	3.3472	0.5879
8	192	2.25	Preparation T	194.2361	-2.2361	-0.3927
9	195	2.25	Standard S	195.3472	-0.3472	-0.0610
10	184	1.5	Standard S	176.5556	7.4444	1.3075
…	…	…	…	…	…	…

Cases marked by ‘**’ are outliers at 2 x Standard Deviation.

Predictions (Interpolations): If, for a case (row) of data, all variables are non-missing, but only the response variable is missing, then the Estimated Response can be calculated using the model parameters (i.e. the common slope and an intercept for each preparation). When a response is predicted, its row label will be prefixed by an asterisk (*).

Likewise, if only the dose value is missing in a row with no other missing values, then the dose value will be calculated using the model parameters When a dose value is predicted, its row label will be prefixed by an ampersand (&).

Such cases are not included in the estimation of the model. Therefore, it will be a good idea to include the cases for which predictions are to be made in the data matrix during the data preparation phase. See section 10.0.7. Prediction, Interpolation, Extrapolation.

Example

In above example case 3 is reported as an outlier at a two standard deviations threshold. Going back to the spreadsheet, deleting the response value of 162 in row 3 and running the analysis again, we obtain a predicted value of 176.2353 for the omitted outlier.

Case (Diagnostic) Statistics

	Response	Dose	Preparations	Estimated Response	Residuals	Standardised Residuals
1	161	1	Standard S	157.7639	3.2361	0.6176
2	151	1	Preparation T	157.4436	-6.4436	-1.2298
* 3	*	1.5	Preparation T	176.2353	*	*
4	194	2.25	Standard S	195.3472	-1.3472	-0.2571
5	176	1.5	Standard S	176.5556	-0.5556	-0.1060
6	193	2.25	Preparation T	195.0270	-2.0270	-0.3869
7	160	1	Preparation T	157.4436	2.5564	0.4879
8	192	2.25	Preparation T	195.0270	-3.0270	-0.5777
9	195	2.25	Standard S	195.3472	-0.3472	-0.0663
10	184	1.5	Standard S	176.5556	7.4444	1.4208
…	…	…	…	…	…	…

Cases marked by ‘*’ are predicted.

10.1.2.4. Comparison of Slopes

If an assay with two or more test preparations is found to depart from parallelism significantly, then we ask the question which test preparation’s slope differs from the slope of the standard preparation. A Dunnett’s multiple comparison test is performed to answer this question.

Here we perform a Dunnett Test, Comparisons against a Control Group option, using the slope values from Separate Regression. For details see 7.4.3.8. Dunnett test.

The slopes test described in European Pharmacopoeia (1997-2017) employs a slightly different algorithm, which is only valid for 2, 3 or 4-dose assays. It is based on linear contrasts as a proxy for actual slopes. The two approaches are identical and produce the same probability values. UNISTAT does not have a limitation on the number of distinct dose values.

European Pharmacopoeia (1997-2017) calculates the test statistic q’ for each test preparation using linear contrasts:

   

     

where:

L₁ is the linear contrast for the standard preparation,

L_i is the linear contrast for the i^th test preparation and

s² is the residual mean square value from the ANOVA table (i.e. sum of squares for the overall residual term divided by its degrees of freedom)

The two-tailed probability for the test statistic is generated using an algorithm developed by Charles Dunnett (Algorithm AS 251) for α significance level, (h – 1) number of groups. The degrees of freedom is equal to that of the overall residual term of the ANOVA table.

Example

Comparison of Slopes

 

Comparison	Difference	Standard Error	q Stat	Table q	Probability
Preparation T – Standard S	4.3160	5.9453	0.7260	2.0423	0.4735

 

Comparison	Lower 95%	Upper 95%	Pass/Fail
Preparation T – Standard S	-7.8259	16.4580	Pass

 

10.1.2.5. Validity of Assay

This output option displays an Analysis of Variance (ANOVA) table, which is used to test the Validity of Assay. The residual sum of squares and its degrees of freedom are used in estimating the confidence limits for the Potency (see section 10.1.2.6. Potency). The three basic tests performed are (i) significance of regression, (ii) parallelism and (iii) linearity. The table may have different entries in its rows depending on the number of doses and / or the ANOVA model employed.

The notation below is for balanced designs as given by European Pharmacopoeia (1997-2017). For unbalanced designs, the only difference is that the sums are taken up to the maximum number of observations in each treatment group, which can be different. See 10.2. Slope Ratio Method, section 10.2.2.4. Validity of Assay for a general unbalanced formulation.

Let us first define the constant term:

     

which is the sum total of all cases divided by the total number of treatment groups, the Treatments term:

     

which is the sum of all squared treatment totals minus the constant term, and the Total term:

     

which is the sum of all squared cases minus the constant term. The rest of table entries are defined as in the following table. Note that instead of reporting linearity and parallelism, we always report non-linearity and non-parallelism, so that when an F-test gives a significant result (i.e. a low P-value), it means that a data set is not linear or two or more data sets are not parallel. Where possible, we also report non-linearity tests for individual preparations, as well as the overall non-linearity for all preparations.

If you do not wish to display the individual non-linearity values for preparations enter the following line:

   NonLinPrepDisp=0

under the [Bioassay] section of this file:

C:\ProgramData\Unistat\Unistat10\Unistat10.ini

Likewise, you can also enter the following line:

   QuadraticDisp=0

not to display the Quadratic Regression information on the table:

 

	Degrees of Freedom	2-dose	3-dose	4-dose
Preparations	h – 1
Linear Regression	1
Non-parallelism	h – 1
Non-linearity	h for 3-dose 2h for 4-dose
Quadratic Regression	1
Difference of Quadratics	h – 1
Residual	h
Treatments	k – 1	M	M	M
Residual		R	R	R
Total	nk – 1	T	T	T

 

The following relationships should always be true:

1)    Degrees of freedom and sum of squares for the first four rows (i.e. Preparations, Linear Regression, Non-parallelism and Non-linearity) should always add up to Treatments,

2)    Quadratic Regression, Difference of Quadratics and their Residuals should always add up to Non-linearity,

3)    Treatments (including plate, row and column effects) and their Residuals should always add up to Total.

All four ANOVA methods supported here differ only in their residual terms, where the residual for the latter two designs contain a Row Block term, which is defined as:

    

where:

    

The Latin Square Design also contains a Column Block term, which is defined as:

    

where:

    

Although the sum of squares and degrees of freedom here are not different from that of Completely Randomised Design, F-statistics and their probability values will be different, as these values are based on the residual sum of squares and degrees of freedom found after removing the effects of Row and Column blocks.

The Crossover Design is different from others in that the column factor usually represents time periods for different treatments and the model includes interaction terms between this variable and others. If the Dose variable has only two values for each preparation then the model is called Twin Crossover Design and it contains interactions between the column factor and Preparations, Linear Regression and Non-Parallelism terms. If there are three dose levels for each preparation, the model is called Triple Crossover Design and it contains additional interactions between the column factor and Quadratic Regression and Quadratic Difference terms.

The Validity of Assay output has different entries for different ANOVA Designs and for different number of dose units used. See 10.2.3. Slope Ratio Examples for different types.

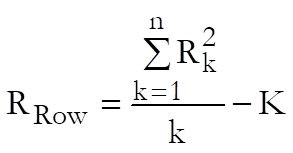
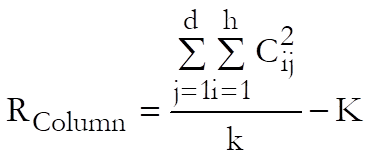
Example

Validity of Assay

Due To	Sum of Squares	DoF	Mean Square	F-Stat	Prob	Pass/Fail
Preparations	11.111	1	11.111	0.535	0.4730	**Fail**
Linear Regression	8475.042	1	8475.042	408.108	0.0000	Pass
Non-parallelism	18.375	1	18.375	0.885	0.3581	Pass
Non-linearity	5.472	2	2.736	0.132	0.8773	Pass
Standard S Non-linearity	0.028	1	0.028	0.001	0.9712	Pass
Preparation T Non-linearity	5.444	1	5.444	0.262	0.6142	Pass
Quadratic Regression	3.125	1	3.125	0.150	0.7022
Quadratic Difference	2.347	1	2.347	0.113	0.7402
Treatments	8510.000	5	1702.000	81.958	0.0000	Pass
Blocks(Rows)	412.000	5	82.400	3.968	0.0116
Blocks(Columns)	218.667	5	43.733	2.106	0.1069
Residual	415.333	20	20.767
Total	9556.000	35	273.029

 

Pass/Fail test results for F-tests are optional. For how to select which tests to perform and how to change the default threshold probability values see section 10.0.5.1. Compliance Output.

10.1.2.6. Potency

By default, the program estimates the potency ratio and its confidence limits employing the generalised algorithm given in Finney (1978), which works with unbalanced, symmetric and balanced designs. European Pharmacopoeia (1997-2017) gives a more restrictive algorithm for balanced assays only. The logarithm of potency ratio is estimated for each test preparation, using the Common Regression slope b.

     

and:

     

where:

     

are the preparation means and A_i is the assumed potency of each test preparation. The estimated potency is the antilog of M, Exp(M).

The method of estimating the confidence interval for potency is based on Fieller’s Theorem (see Finney 1978, p. 80). Let us first define the correction factor g as:

     

where E is the sum of squares for the Linear Regression term and s² is the residual mean squares from the ANOVA table.  is the critical value from the t-distribution with the same degrees of freedom. The confidence limits computed below are reliable for g < 1. If this condition is not fulfilled, the program will issue a warning message, but still display the confidence limits computed.

The log of confidence limits for the potency ratio of each test preparation is defined as:

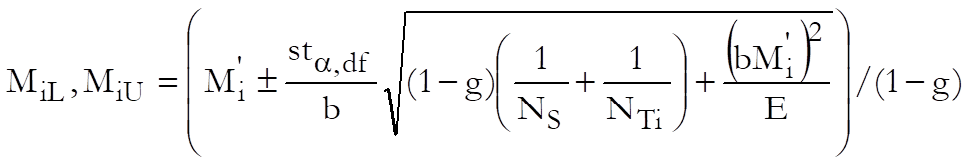
where the variance of M_i is:

     

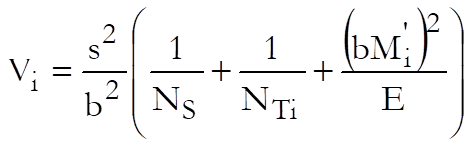
Weights are computed after the estimated potency and its confidence interval are found:

     

and % Precision is:

     

According to European Pharmacopoeia (1997) the common slope b is calculated as:

     

     

Where:

      Z = Log(dose_i+1) – Log(dose_i), i = 2, … , d

is the log of successive dose ratios. Also define a correction factor:

     

where E is the sum of squares for the Linear Regression term and s² is the residual mean squares and  is the critical value from the t-distribution with degrees of freedom of the overall residual term from the ANOVA table.

The log of the corrected potency estimate and its confidence intervals are computed as:

where:

     

The only difference from the default output here is reporting of C and H constants for validation purposes, where C = 1 / (1 – g).

If the data column [Dose] contains the actual dose levels administered in original dose units, we will obtain the estimated potency and its confidence limits in the same units. If, however, the [Dose] column contains unitless relative dose levels, then we may need to perform further calculations to obtain the estimated potency in original units. To do that you can enter assigned potency of the standard, assumed potency of each test preparation and pre-dilutions for all preparations including the standard in a data column and select it as [Dilution] variable. UNISTAT will then calculate the estimated potency as described in section 10.0.2. Doses, Dilutions and Potency. Also see section 10.0.3. Potency Calculation Example.

Example

Potency

Latin Squares Design

	Estimated Potency	Lower 95%	Upper 95%	DoF	% Precision
Preparation T	0.9763	0.9112	1.0456	20	93.33%

 

	Relative Potency	Lower 95%	Upper 95%
Preparation T	97.63%	91.12%	104.56%

 

	Percent CI	Lower 95%	Upper 95%	Pass/Fail
Preparation T	100.00%	93.33%	107.09%	Pass

PotencyPctLower: 93.3289382317094 GT 75 Pass

AND

PotencyPctUpper: 107.0925498258 LT 125 Pass

 

G =	0.0107
C =	1.0108

 

Almost all items on this output are optional. The Pass/Fail column on Percent Confidence Interval tests whether the lower limit is greater than 75% AND the upper limit is less than 125% by default. If one of these two results is Fail, then the overall result will also be Fail. These default percentage values can be changed by the user. It is also possible to test only the lower limit against a given lower threshold or only the upper limit against another upper threshold. For details see section 10.0.5.1. Compliance Output.

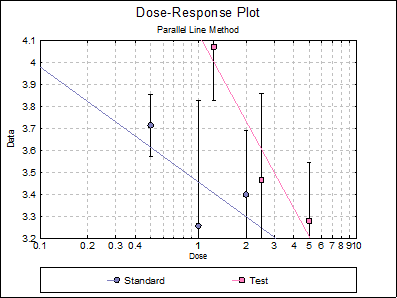
10.1.2.7. Dose-Response Plot

By default, this option generates a plot of treatment means against the log of dose, with standard error bars for each mean. Each preparation will be plotted as one data series, with as many points as the number of doses applied. A line of best fit and its confidence limits will be drawn for each series. This provides a visual means of inspecting the data, enabling the user to notice immediately whether there is something substantially wrong with the data.

Alternatively, individual response values can be plotted against the log of dose, all with or without trend lines and confidence intervals.

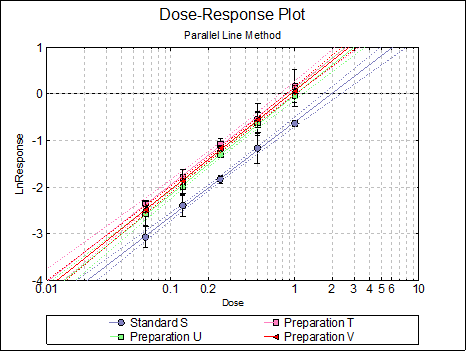
Clicking the [Opt] button situated to the left of Dose-Response Plot output option will place the graph in UNISTAT’s Graphics Editor. Here, all aspects of the graph can be edited and customised.

Selecting Edit → Dose-Response Plot… (or double-clicking on the graph area) will pop a dialogue where what is displayed on the plot can be controlled.

If you uncheck the Treatment means with error bars box, individual response values will be plotted against the log of dose.

 

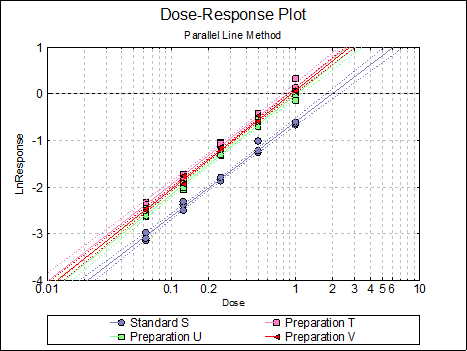
10.1.3. Parallel Line Examples

The following Parallel Line Method examples are based on different Analysis of Variance methods. Data sets were entered into UNISTAT’s spreadsheet and necessary data manipulations made by using UNISTAT spreadsheet functions (see 10.0.1. Data Preparation and 10.0.2. Doses, Dilutions and Potency). Final data sets were saved in two files; BIOPHARMA9 which contains examples from European Pharmacopoeia (2017, the 9^th Edition) and BIOFINNEY containing examples from Finney (1978).

10.1.3.1. Completely Randomised Design with 2 Doses and 3 Preparations

Data is given in Table 5.1.1-I. on p. 4364 of European Pharmacopoeia (9^th Edition).

Open BIOPHARMA9 and select Bioassay → Parallel Line Method. From the Variable Selection Dialogue select the first option Completely Randomised Design and then select columns C1, C2 and L3 respectively as [Data], [Dose] and [Preparation]. Click [Next] to proceed to Output Options Dialogue. Click [All] to perform all tests in one go and click [Finish]. The following output is obtained:

Parallel Line Method

Valid Number of Cases: 60, 0 Omitted

Completely Randomised Design

Summary Statistics

Data variable: Response

Subsample selected by: Dose x Preparations

	Valid Cases	Mean	Variance	Standard Error
0.25 x Standard S	10	332.0000	1026.6667	10.1325
0.25 x Preparation T	10	323.9000	724.9889	8.5146
0.25 x Preparation U	10	282.2000	854.6222	9.2446
1 x Standard S	10	248.4000	483.8222	6.9557
1 x Preparation T	10	244.0000	718.6667	8.4774
1 x Preparation U	10	250.0000	784.6667	8.8581

 

Anderson-Darling Normality Test

Alpha = 0.05

Dose x Preparations	Test Statistic	Probability	Pass/Fail
0.25 x Standard S	0.2218	0.7658	Pass
0.25 x Preparation T	0.2311	0.7326	Pass
0.25 x Preparation U	0.5030	0.1549	Pass
1 x Standard S	0.3494	0.3962	Pass
1 x Preparation T	0.2337	0.7232	Pass
1 x Preparation U	0.2055	0.8201	Pass

 

Homogeneity of Variance Tests

For 6 groups defined by Dose x Preparations.

Alpha = 0.05

	Test Statistic	Probability	Pass/Fail
Levene’s F Test	0.3738	0.8644	Pass

 

Dixon’s Outlier Test

Alpha = 0.05

One-tailed tests

Dose x Preparations	Dixon’s Q	Table Q	Pass/Fail
0.25 x Standard S Q(Min)	0.1351	0.4779	Pass
Q(Max)	0.2889	0.4779	Pass
0.25 x Preparation T Q(Min)	0.0714	0.4779	Pass
Q(Max)	0.1333	0.4779	Pass
0.25 x Preparation U Q(Min)	0.1299	0.4779	Pass
Q(Max)	0.0429	0.4779	Pass
1 x Standard S Q(Min)	0.1667	0.4779	Pass
Q(Max)	0.3333	0.4779	Pass
1 x Preparation T Q(Min)	0.0857	0.4779	Pass
Q(Max)	0.1351	0.4779	Pass
1 x Preparation U Q(Min)	0.0429	0.4779	Pass
Q(Max)	0.1410	0.4779	Pass

N = 10, Q(Min)=(X(2)-X(1))/(X(N-1)-X(1)), Q(Max)=(X(N)-X(N-1))/(X(N)-X(2))

 

 

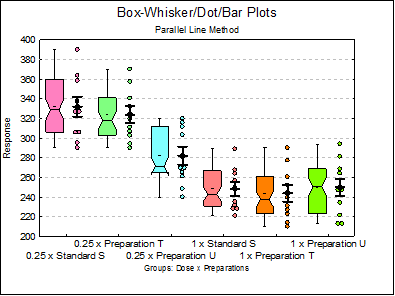
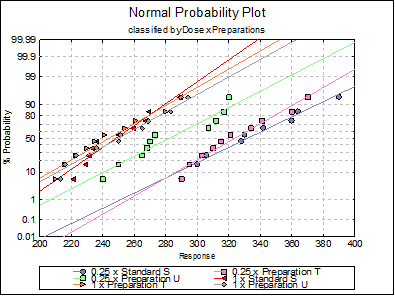
Separate Regression

	Intercept	Slope	Residual SS	R-squared
Standard S	248.4000	-60.3047	13594.4000	0.7199
Preparation T	244.0000	-57.6357	12992.9000	0.7107
Preparation U	250.0000	-23.2274	14753.6000	0.2600

 

Common Regression

	Intercept	Slope	Residual SS	R-squared
Standard S	257.5833	-47.0559	49559.1333	0.5629
Preparation T	251.3333
Preparation U	233.4833

 

Residual Variance =	884.9845
Degrees of Freedom =	56

 

Case (Diagnostic) Statistics

	Response	Dose	Preparations	Estimated Response	Residuals	Standardised Residuals
1	300	0.25	Standard S	322.8167	-22.8167	-0.7670
2	310	0.25	Standard S	322.8167	-12.8167	-0.4308
3	330	0.25	Standard S	322.8167	7.1833	0.2415
4	290	0.25	Standard S	322.8167	-32.8167	-1.1031
5	364	0.25	Standard S	322.8167	41.1833	1.3844
6	328	0.25	Standard S	322.8167	5.1833	0.1742
** 7	390	0.25	Standard S	322.8167	67.1833	2.2584
8	360	0.25	Standard S	322.8167	37.1833	1.2499
9	342	0.25	Standard S	322.8167	19.1833	0.6448
10	306	0.25	Standard S	322.8167	-16.8167	-0.5653
11	289	1	Standard S	257.5833	31.4167	1.0561
12	221	1	Standard S	257.5833	-36.5833	-1.2297
13	267	1	Standard S	257.5833	9.4167	0.3165
…	…	…	…	…	…	…

Cases marked by ‘**’ are outliers at 2 x Standard Deviation.

Comparison of Slopes

Comparison	Difference	Standard Error	q Stat	Table q
Preparation U – Standard S	37.0773	12.6231	2.9372	2.2713
Preparation T – Standard S	2.6690	12.6231	0.2114	2.2713

 

Comparison	Probability	Lower 95%	Upper 95%	Result
Preparation U – Standard S	0.0093	8.4061	65.7484	**Fail**
Preparation T – Standard S	0.9678	-26.0022	31.3401	Pass

 

Validity of Assay

Due To	Sum of Squares	DoF	Mean Square	F-Stat	Prob
Preparations	6256.633	2	3128.317	4.086	0.0223
Linear Regression	63830.817	1	63830.817	83.377	0.0000
Non-parallelism	8218.233	2	4109.117	5.367	0.0075
Non-linearity	0.000	0
Treatments	78305.683	5	15661.137	20.457	0.0000
Residual	41340.900	54	765.572
Total	119646.583	59	2027.908

 

Potency

	Estimated Potency	Lower 95%	Upper 95%	DoF	% Precision
Preparation T	1.1420	0.7836	1.6869	54	68.62%
Preparation U	1.6689	1.1481	2.5550	54	68.80%

 

	Relative Potency	Lower 95%	Upper 95%
Preparation T	114.20%	78.36%	168.69%
Preparation U	166.89%	114.81%	255.50%

 

	Percent CI	Lower 95%	Upper 95%
Preparation T	100.00%	68.62%	147.71%
Preparation U	100.00%	68.80%	153.10%

 

G =	0.0482
C =	1.0507

 

 

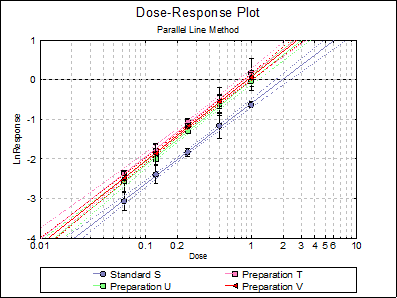
Looking at the plot of treatment means we can see that Preparation U line is not nearly parallel to Standard S and Preparation T lines. This can also be picked up from the non-parallelism test in Validity of Assay (0.0075), which is significant at 5% level. The Comparison of Slopes test also reports a significant difference between Preparation U and Standard S slopes.

This assay can still be useful by omitting Preparation U and performing the analysis for Standard S and Preparation U. In Excel Add-In Mode, you can simply select the block A1:C41 and repeat the analysis. In Stand-Alone Mode, you can define a Select Row column to omit these rows from the analysis, without actually deleting them from the spreadsheet. To do this, click somewhere on column 4, and select Data → Select Row option from UNISTAT’s spreadsheet menus. The colour of C4 will change. This indicates that all rows with a 0 entry in this column will be omitted from the subsequent analyses.

When the analysis is repeated without Preparation U, the following results are obtained:

Parallel Line Method

Rows 41-60 Omitted

Selected by C4 Select

 

Valid Number of Cases: 40, 20 Omitted

Completely Randomised Design

Separate Regression

	Intercept	Slope	Residual SS	R-squared
Standard S	248.4000	-60.3047	13594.4000	0.7199
Preparation T	244.0000	-57.6357	12992.9000	0.7107

 

Common Regression

	Intercept	Slope	Residual SS	R-squared
Standard S	249.3250	-58.9702	26621.5250	0.7151
Preparation T	243.0750

 

Residual Variance =	719.5007
Degrees of Freedom =	37

 

Comparison of Slopes

Comparison	Difference	Standard Error	q Stat	Table q
Preparation T – Standard S	2.6690	12.3983	0.2153	2.0281

 

Comparison	Probability	Lower 95%	Upper 95%	Result
Preparation T – Standard S	0.8308	-22.4759	27.8138	Pass

 

Validity of Assay

Due To	Sum of Squares	DoF	Mean Square	F-Stat	Prob
Preparations	390.625	1	390.625	0.529	0.4718
Linear Regression	66830.625	1	66830.625	90.491	0.0000
Non-parallelism	34.225	1	34.225	0.046	0.8308
Non-linearity	0.000	0
Treatments	67255.475	3	22418.492	30.355	0.0000
Residual	26587.300	36	738.536
Total	93842.775	39	2406.225

 

Potency

	Estimated Potency	Lower 95%	Upper 95%	DoF	% Precision
Preparation T	1.1118	0.8250	1.5136	36	74.20%

 

	Relative Potency	Lower 95%	Upper 95%
Preparation T	111.18%	82.50%	151.36%

 

	Percent CI	Lower 95%	Upper 95%
Preparation T	100.00%	74.20%	136.14%

 

G =	0.0455
C =	1.0476

 

 

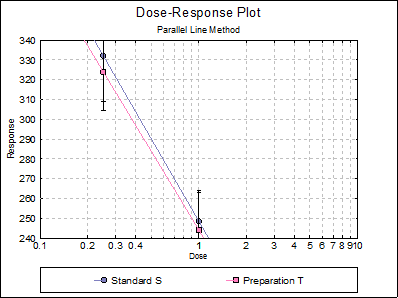
In Stand-Alone Mode, do not forget to reset column 4, otherwise the Select Row function will be effective in subsequent procedures you run. To do this, click somewhere on column 4, and select Data → Select Row option again, or select Formula → Quick Formula from the menu and enter data. The colour of C4 will change back to its original state.

10.1.3.2. Completely Randomised Design with 5 Doses and 4 Preparations

Data is given in Table 5.1.4-I. on p. 4367 of European Pharmacopoeia (9^th Edition).

Open BIOPHARMA9 and select Bioassay → Parallel Line Method. From the Variable Selection Dialogue select the first option Completely Randomised Design and then select columns C17, C18, L19 and L20 respectively as [Data], [Dose], [Preparation] and [Dilution]. Click [Next] to proceed to Output Options Dialogue, select only the following output options and click [Finish]:

Parallel Line Method

Valid Number of Cases: 60, 0 Omitted

Completely Randomised Design

Separate Regression

	Intercept	Slope	Residual SS	R-squared
Standard S	-0.5998	0.8813	0.0904	0.9920
Preparation T	0.1355	0.9037	0.1208	0.9898
Preparation U	-0.0226	0.9278	0.0843	0.9933
Preparation V	0.0714	0.9211	0.0459	0.9963

 

Common Regression

	Intercept	Slope	Residual SS	R-squared
Standard S	-0.5621	0.9085	0.3600	0.9925
Preparation T	0.1422
Preparation U	-0.0495
Preparation V	0.0539

 

Residual Variance =	0.0065
Degrees of Freedom =	55

 

Comparison of Slopes

Comparison	Difference	Standard Error	q Stat	Table q
Preparation U – Standard S	0.0466	0.0304	1.5296	2.4415
Preparation V – Standard S	0.0398	0.0304	1.3074	2.4415
Preparation T – Standard S	0.0224	0.0304	0.7365	2.4415

 

Comparison	Probability	Lower 95%	Upper 95%	Result
Preparation U – Standard S	0.3036	-0.0278	0.1209	Pass
Preparation V – Standard S	0.4262	-0.0345	0.1141	Pass
Preparation T – Standard S	0.8033	-0.0519	0.0967	Pass

 

Validity of Assay

Due To	Sum of Squares	DoF	Mean Square	F-Stat	Prob
Preparations	4.475	3	1.492	223.395	0.0000
Linear Regression	47.584	1	47.584	7125.912	0.0000
Non-parallelism	0.019	3	0.006	0.933	0.4339
Non-linearity	0.074	12	0.006	0.926	0.5307
Standard S Non-linearity	0.017	3	0.006	0.850	0.4747
Preparation T Non-linearity	0.028	3	0.009	1.410	0.2538
Preparation U Non-linearity	0.018	3	0.006	0.886	0.4564
Preparation V Non-linearity	0.011	3	0.004	0.559	0.6455
Treatments	52.152	19	2.745	411.053	0.0000
Residual	0.267	40	0.007
Total	52.419	59	0.888

 

Potency

Assumed potency of Preparation T: 20 µg protein/ml

Assumed potency of Preparation U: 20 µg protein/ml

Assumed potency of Preparation V: 20 µg protein/ml

 

	Estimated Potency	Lower 95%	Upper 95%
Preparation T	43.4197	40.5448	46.5397
Preparation U	35.1628	32.8697	37.6403
Preparation V	39.4018	36.8126	42.2058

 

	Relative Potency	Lower 95%	Upper 95%
Preparation T	217.10%	202.72%	232.70%
Preparation U	175.81%	164.35%	188.20%
Preparation V	197.01%	184.06%	211.03%

 

	Percent CI	Lower 95%	Upper 95%
Preparation T	100.00%	93.38%	107.19%
Preparation U	100.00%	93.48%	107.05%
Preparation V	100.00%	93.43%	107.12%

 

G =	0.0006
C =	1.0006

 

 

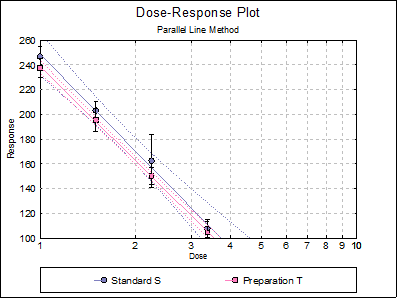
10.1.3.3. Randomised Block Design with 4 Doses and 2 Preparations

Data is given in Table 5.1.3.-I on p. 4366 of European Pharmacopoeia (9^th Edition).

Open BIOPHARMA9 and select Bioassay → Parallel Line Method. From the Variable Selection Dialogue select the second option Randomised Block Design and the select columns C11, C12, L13, C14 and L15 respectively as [Data], [Dose], [Preparation], [Row Factor] and [Dilution]. Click [Next] to proceed to the Output Options Dialogue.

Parallel Line Method

Valid Number of Cases: 40, 0 Omitted

Randomised Block Design

Separate Regression

	Intercept	Slope	Residual SS	R-squared
Standard S	248.5800	-113.0060	1897.7400	0.9651
Preparation T	238.5000	-109.5039	747.8000	0.9851

 

Common Regression

	Intercept	Slope	Residual SS	R-squared
Standard S	247.5150	-111.2549	2670.7450	0.9744
Preparation T	239.5650

 

Comparison of Slopes

Comparison	Difference	Standard Error	q Stat	Table q
Preparation T – Standard S	3.5022	5.1221	0.6837	2.0484

 

Comparison	Probability	Lower 95%	Upper 95%	Result
Preparation T – Standard S	0.4998	-6.9901	13.9944	Pass

 

Validity of Assay

Due To	Sum of Squares	DoF	Mean Square	F-Stat	Prob
Preparations	632.025	1	632.025	11.722	0.0019
Linear Regression	101745.605	1	101745.605	1887.111	0.0000
Non-parallelism	25.205	1	25.205	0.467	0.4998
Non-linearity	259.140	4	64.785	1.202	0.3321
Standard S Non-linearity	238.140	2	119.070	2.208	0.1287
Preparation T Non-linearity	21.000	2	10.500	0.195	0.8241
Quadratic Regression	148.225	1	148.225	2.749	0.1085
Quadratic Difference	34.225	1	34.225	0.635	0.4323
Residual	76.690	2	38.345
Treatments	102661.975	7	14665.996	272.015	0.0000
Blocks(Rows)	876.750	4	219.188	4.065	0.0101
Residual	1509.650	28	53.916
Total	105048.375	39	2693.548

 

Potency

Randomised Block Design

Assigned potency of Standard S: 670 IU/mg

Pre-dilution of Standard S: 16.7 mg / 25 ml; 1 ml / 40 ml

Assumed potency of Preparation T: 20000 IU/vial

Pre-dilution of Preparation T: 1 vial / 40 ml; 1 ml / 40 ml

 

	Estimated Potency	Lower 95%	Upper 95%
Preparation T	19228.4755	18423.3508	20075.1776

 

	Relative Potency	Lower 95%	Upper 95%
Preparation T	107.41%	102.91%	112.14%

 

	Percent CI	Lower 95%	Upper 95%
Preparation T	100.00%	95.81%	104.40%

 

G =	0.0022
C =	1.0022

 

 

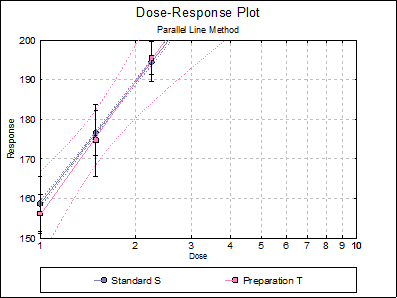
10.1.3.4. Latin Square Design with 3 Doses and 2 Preparations

Data is given in Table 5.1.2.-II on p. 4367 of European Pharmacopoeia (9^th Edition).

The entry and transformation of this data set is more complicated than the two previous examples. In order to assign the correct dose levels and preparation groups, information given in Table 5.1.2.-I is essential. Ensure that the way the factor columns are created is understood well.

Open BIOPHARMA9 and select Bioassay → Parallel Line Method. From the Variable Selection Dialogue select the third option Latin Square Design and then select columns C5, C6, L7, C8, C9 and L10 respectively as [Data], [Dose], [Preparation], [Row Factor], [Col Factor] and [Dilution]. Click [Next] to proceed to Output Options Dialogue.

Parallel Line Method

Valid Number of Cases: 36, 0 Omitted

Latin Squares Design

Separate Regression

	Intercept	Slope	Residual SS	R-squared
Standard S	158.6389	44.1879	478.3611	0.8895
Preparation T	155.7778	48.5040	573.1111	0.8901

 

Common Regression

	Intercept	Slope	Residual SS	R-squared
Standard S	157.7639	46.3460	1069.8472	0.8879
Preparation T	156.6528

 

Residual Variance =	32.4196
Degrees of Freedom =	33

 

Comparison of Slopes

Comparison	Difference	Standard Error	q Stat	Table q
Preparation T – Standard S	4.3160	4.5883	0.9407	2.0860

 

Comparison	Probability	Lower 95%	Upper 95%	Result
Preparation T – Standard S	0.3581	-5.2551	13.8871	Pass

 

Validity of Assay

Due To	Sum of Squares	DoF	Mean Square	F-Stat	Prob
Preparations	11.111	1	11.111	0.535	0.4730
Linear Regression	8475.042	1	8475.042	408.108	0.0000
Non-parallelism	18.375	1	18.375	0.885	0.3581
Non-linearity	5.472	2	2.736	0.132	0.8773
Standard S Non-linearity	0.028	1	0.028	0.001	0.9712
Preparation T Non-linearity	5.444	1	5.444	0.262	0.6142
Quadratic Regression	3.125	1	3.125	0.150	0.7022
Quadratic Difference	2.347	1	2.347	0.113	0.7402
Treatments	8510.000	5	1702.000	81.958	0.0000
Blocks(Rows)	412.000	5	82.400	3.968	0.0116
Blocks(Columns)	218.667	5	43.733	2.106	0.1069
Residual	415.333	20	20.767
Total	9556.000	35	273.029

 

Potency

Latin Squares Design

Assigned potency of Standard S: 4855 IU/mg

Pre-dilution of Standard S: 25.2 mg / 24.5 ml

Assumed potency of Preparation T: 5600 IU/mg

Pre-dilution of Preparation T: 21.4 mg / 23.95 ml

 

	Estimated Potency	Lower 95%	Upper 95%
Preparation T	5456.3665	5092.3689	5843.3620

 

	Relative Potency	Lower 95%	Upper 95%
Preparation T	97.63%	91.12%	104.56%

 

	Percent CI	Lower 95%	Upper 95%
Preparation T	100.00%	93.33%	107.09%

 

G =	0.0107
C =	1.0108

 

 

10.1.3.5. Twin Crossover Design

Data is given in Table 5.1.5-II. on p. 4368 of European Pharmacopoeia (9^th Edition).

Open BIOPHARMA9 and select Bioassay → Parallel Line Method. From the Variable Selection Dialogue select the fourth option Crossover Design and select columns C21, C22, L23, C24, C25 and L26 respectively as [Data], [Dose], [Preparation], [Row Factor] and [Col Factor]. Click [Next] to proceed to Output Options Dialogue and then click [Finish]. The following output is obtained:

Parallel Line Method

Valid Number of Cases: 64, 0 Omitted

Crossover Design

Separate Regression

	Intercept	Slope	Residual SS	R-squared
Standard	101.1875	-47.6991	19294.1875	0.3119
Test	91.5625	-20.1977	23815.8750	0.0618

 

Common Regression

	Intercept	Slope	Residual SS	R-squared
Standard	96.4219	-33.9484	44563.5781	0.1658
Test	96.3281

 

Residual Variance =	730.5505
Degrees of Freedom =	61

 

Comparison of Slopes

Comparison	Difference	Standard Error	q Stat	Table q
Test – Standard	27.5014	8.4520	3.2538	2.0484

 

Comparison	Probability	Lower 95%	Upper 95%	Result
Test – Standard	0.0030	10.1882	44.8146	**Fail**

 

Validity of Assay

Due To	Sum of Squares	DoF	Mean Square	F-Stat	Prob
Non-parallelism	1453.5156	1	1453.5156	1.0638	0.3112
DaysxPreparations	31.6406	1	31.6406	0.0232	0.8801
DaysxLinear Regression	50.7656	1	50.7656	0.0372	0.8485
Error Between	38258.8125	28	1366.3862
Blocks(Rows)	39794.7344	31	1283.7011
Preparations	0.1406	1	0.1406	0.0010	0.9747
Linear Regression	8859.5156	1	8859.5156	64.5324	0.0000
Days	478.5156	1	478.5156	3.4855	0.0724
DaysxNon-parallelism	446.2656	1	446.2656	3.2506	0.0822
Error Within	3844.0625	28	137.2879
Total	53423.2344	63	847.9878

 

Potency

Crossover Design

Assumed potency of Test: 40 IU/ml

 

	Estimated Potency	Lower 95%	Upper 95%
Test	40.1106	33.4162	48.1646

 

	Relative Potency	Lower 95%	Upper 95%
Test	100.28%	83.54%	120.41%

 

	Percent CI	Lower 95%	Upper 95%
Test	100.00%	83.31%	120.08%

 

G =	0.0650
C =	1.0695

 

 

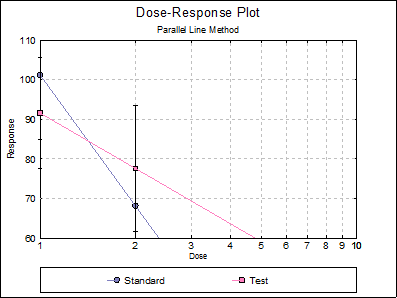
Although the plot of treatment means and the Comparison of Slopes test seem to indicate deviation from parallelism, the non-parallelism test in Validity of Assay (0.3112) is not significant at 5% level.

10.1.3.6. Triple Crossover Design

Table 10.3.1. on p. 205 from Finney, D. J. (1978) is an example with three dose levels and two preparations.

Open BIOFINNEY and select Bioassay → Parallel Line Method. From the Variable Selection Dialogue select the fourth option Crossover Design and select columns C15, C16, S17, C18 and C19 respectively as [Data], [Dose], [Preparation], [Row Factor] and [Col Factor]. Click [Next] to proceed to Output Options Dialogue and click [Finish].

Parallel Line Method

Valid Number of Cases: 60, 0 Omitted

Crossover Design

Separate Regression

	Intercept	Slope	Residual SS	R-squared
Standard	3.4547	-0.2272	8.1200	0.0576
Test	4.1272	-0.5713	5.2830	0.3725

 

Common Regression

	Intercept	Slope	Residual SS	R-squared
Standard	3.4547	-0.3993	13.9718	0.1798
Test	3.9695

 

Residual Variance =	0.2451
Degrees of Freedom =	57

 

Comparison of Slopes

Comparison	Difference	Standard Error	q Stat	Table q
Test – Standard	-0.3441	0.1209	2.8455	2.0639

 

Comparison	Probability	Lower 95%	Upper 95%	Result
Test – Standard	0.0089	-0.5937	-0.0945	**Fail**

 

Validity of Assay

Due To	Sum of Squares	DoF	Mean Square	F-Stat	Prob
Non-parallelism	0.5688	1	0.5688	1.6032	0.2176
Quadratic Regression	0.8687	1	0.8687	2.4484	0.1307
DaysxPreparations	0.3481	1	0.3481	0.9810	0.3318
DaysxLinear Regression	0.0031	1	0.0031	0.0086	0.9267
DaysxQuadratic Difference	1.9026	1	1.9026	5.3624	0.0294
Error Between	8.5153	24	0.3548
Blocks(Rows)	12.2066	29	0.4209
Preparations	0.3330	1	0.3330	4.7403	0.0395
Linear Regression	3.0636	1	3.0636	43.6087	0.0000
Days	0.0150	1	0.0150	0.2141	0.6477
Quadratic Difference	0.0261	1	0.0261	0.3716	0.5478
DaysxNon-parallelism	0.0164	1	0.0164	0.2335	0.6333
DaysxQuadratic Regression	0.0216	1	0.0216	0.3075	0.5844
Error Within	1.6861	24	0.0703
Total	17.3685	59	0.2944

 

Potency

	Estimated Potency	Lower 95%	Upper 95%
Test	0.2754	0.1783	0.3923

 

G =	0.0977
C =	1.1083