7.3.1. Analysis of Variance
This section concentrates on operational aspects of the procedure ANOVA. The following types of experimental design that can be estimated using this procedure have been explained in detail above with solved examples (see 7.3.0.2. ANOVA Designs):
Of the four ANOVA dialogues described in this section, two are conditional upon selection of variables in the first dialogue. The ANOVA Design dialogue will not appear unless a [Repeated] column is selected and the interaction selection dialogue will not appear unless two or more [Factor] columns are selected.
UNISTAT’s ANOVA procedure can cope with unbalanced designs where the number of observations in cells are not necessarily equal. Data may contain missing values and / or missing cells. Factor columns may be numeric, string, date or time variables and need not be sorted. It is possible to select an unlimited number of dependent variables, factors, repeated measures and covariates. In case more than one dependent variable is selected, the analysis will be repeated for each dependent variable with rest of the settings unchanged.
It is possible to analyse simple factorial, repeated measures, nested and mixed designs using the ANOVA procedure, whose output consists of an Analysis of Variance table. The output options of the more powerful General Linear Model procedure include table of means, coefficients, fitted values and residuals and their plots. It is also possible to perform multiple comparison tests on the GLM model fitted (see 7.3.2. General Linear Model).
7.3.1.1. ANOVA Variable Selection
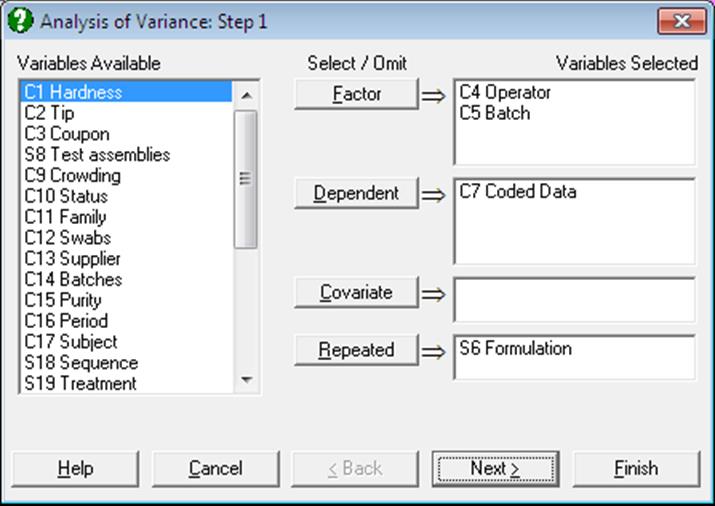
To run an Analysis of Variance, at least one [Factor] column and one [Dependent] column should be selected. [Covariate] and [Repeated] selections are optional.
The variable selection for General Linear Model is slightly different from that of Analysis of Variance. The descriptions of the [Dependent] and [Covariate] buttons are similar, however the [Factor] and [Repeated] buttons are handled differently in GLM (see 7.3.2.1. GLM Variable Selection).
Factor: A factor is a categorical variable (numeric or string) which classifies the data into a number of groups. Analysis of Variance compares the mean value of data in these groups. At least one factor is required and an unlimited number of factors can be selected.
Dependent: It is compulsory to select at least one column containing numeric data. When more than one data variable is selected, the analysis will be repeated as many times as the number of data variables, each time only changing the data variable and keeping the rest of selections unchanged.
Covariate: A covariate is a continuous (noncategorical) numeric variable which may be included in the analysis in order to remove its effect on the dependent variable. Any number of covariates can be selected from the Variables Available list by clicking on [Covariate]. When covariates are included in the analysis, an adjustment is made in the sum of squares for them before any other factors.
Repeated: This button is used to select a repeated measure column or a nested sub-factor on another factor column. The number of repeated measures selected must be less than or equal to the number of factors selected. The repeated measures and Nested Factors are calculated in the same way, but repeated measures are used as an error term to test the significance of the factor and Nested Factors are used as part of the model.
In ANOVA with Repeated Measures over all Factors (see 7.3.1.2.1. Repeated Measures over all Factors) only one factor column is selected with this button. This column defines the repeated measures on all factors.
In ANOVA with Repeated Measures over some Factors (see 7.3.1.2.2. Repeated Measures over some Factors) this button is used to specify repeated measures on the corresponding factors. The first column selected is considered as a repeated measure on the first factor, the second column selected as a repeated measure on the second factor, etc.
In ANOVA with Nested Factors (see 7.3.1.2.3. Nested Factors) this button is used to specify Nested Factors of the main factors. The first column selected is considered as a nested factor of the first factor, the second column selected as nested factor of the second factor, etc.
In ANOVA with Mixed Factors (see 7.3.1.2.4. Mixed Factors) this button is used to specify both repeated measures and Nested Factors. A subsequent dialogue is used to select the columns as repeated measures or Nested Factors.
7.3.1.2. ANOVA Designs
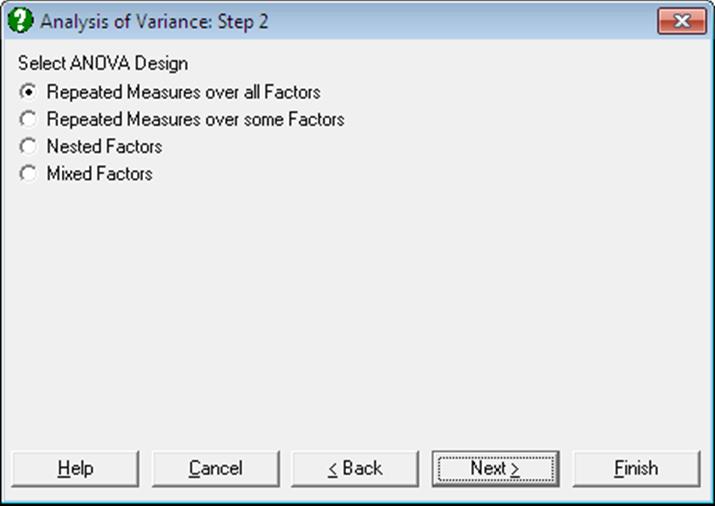
This dialogue does not appear if no columns were selected as [Repeated] in the Variable Selection Dialogue.
7.3.1.2.1. Repeated Measures over all Factors
When this option is selected, the factor selected as [Repeated] will be used to partition the total sum of squares into a between sum of squares and a within sum of squares term. An extra factor called Trial will be added to the model. The Trial sum of squares will be considered to be contained in the Within Subjects sum of squares. All other factors will be considered to be contained in the Between Subjects sum of squares. These are the assumptions for a repeated measures design across all specified factors. See 7.3.0.2.2. Repeated Measures Design and 7.3.0.2.2.1. Repeated Measures over all Factors for a detailed description of these designs.
7.3.1.2.2. Repeated Measures over some Factors
With this option, the factors selected as [Repeated] will be used to specify repeated measures on the main factors. This behaves differently from the Repeated Measures over all Factors option, where only one repeated measure column should be selected.
The first repeated measure selected is considered as a repeated measure on the first factor, the second repeated measure as a repeated measure on the second factor, etc. Repeated measures appear in the ANOVA table as Error(column name) directly under the factor it refers to. The value of the mean square is used as the error term to test the main factor for which it was selected. This procedure is used for Split-Plot design (see 7.3.0.2.5. Split-Plot Design).
7.3.1.2.3. Nested Factors
The factor columns selected as [Repeated] are used here to specify Nested Factors under the main factors. The first nested factor selected is considered as a nested factor of the first factor, the second as a nested factor of the second factor, etc.
Nested Factors appear as nested factor label(main factor label) in the ANOVA table. This procedure is used for Nested Factors designs (see section 7.3.0.2.6. Nested Design).
7.3.1.2.4. Mixed Factors
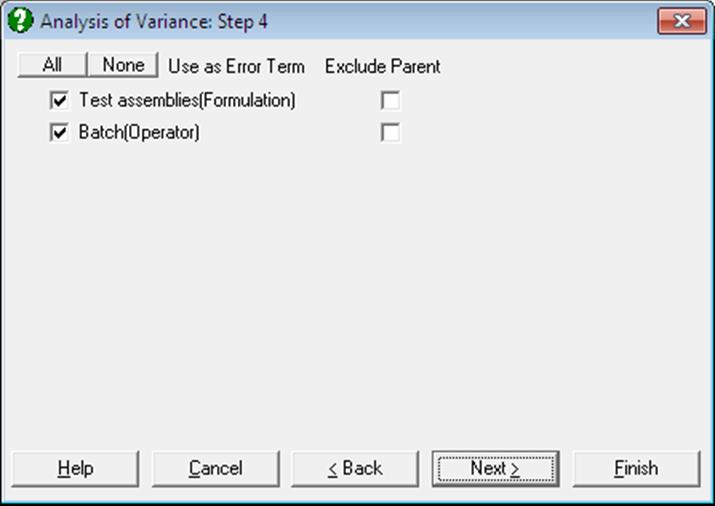
The factor columns selected as [Repeated] are used to specify either repeated measures (see 7.3.1.2.1. Repeated Measures over all Factors) or Nested Factors (see 7.3.1.2.3. Nested Factors) under the main factors. A further dialogue is used to select each term as a repeated measure or a nested factor. If the term is used as an error term, then it is a repeated measure. Otherwise it is a nested factor. The Exclude Parent check box is only applied to Nested Factors and should be left clear. Repeated measures appear in the ANOVA table as Error(column name) directly under the factor it refers to. Nested Factors appear as nested factor label(main factor label).
This procedure is used for Split-Plot design (see 7.3.0.2.5. Split-Plot Design), Nested Factors designs (see section 7.3.0.2.6. Nested Design) and mixtures of the two.
7.3.1.3. ANOVA Approaches
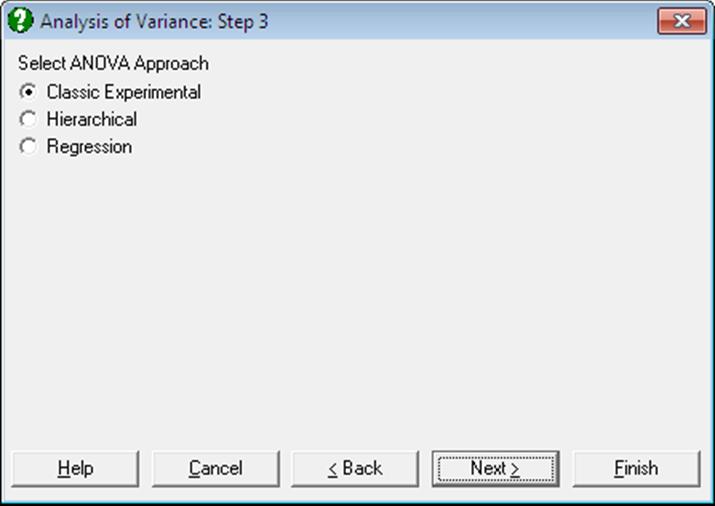
Different approaches may be employed to compute the sum of squares figures displayed in ANOVA tables. The following are the three approaches supported by UNISTAT’s ANOVA procedure. The General Linear Model procedure only supports the Regression Approach.
Classic Experimental Approach: This is probably the most common approach used in unbalanced design Analysis of Variance. It is also called the weighted means solution. For instance, in a three way ANOVA, the sum of squares computed for factors A, B, C and their interactions are calculated after the following adjustments: the main effects after the effects of all the other factors, two-way interactions after all the main effects and all the other two-way effects, and the three-way interactions after all the main effects, all the two-way effects and all the other three-way interactions.
Hierarchical Approach: This is also called the forward sequential solution. Adjustments for the main effects are sequential. For instance, in a three way ANOVA, no adjustment is made for factor A, factor B is adjusted for A, and factor C is adjusted for A and B. The two-way interactions are not sequential. Each one is adjusted for the other two, but not for the main effects. The three-way interaction is adjusted for all main effects and two-way effects. So this approach differs from Classic Experimental Approach only in the way the main effects are calculated.
Regression Approach: This is also called the mean of cell means solution. All effects are computed after an adjustment is made for all other effects. For instance, in a three way ANOVA, a main effect is calculated after an adjustment is made for all other main effects, all two-way effects, the three-way effect, and if any, all covariates and the repeated measure.
The following table shows how the three approaches partition the main effects in a three way analysis of variance.
|
Effect |
Classic Experimental |
Hierarchical |
Regression |
|
A |
A adjusted for B, C |
A |
A adjusted for full model |
|
B |
B adjusted for A, C |
B adjusted for A |
B adjusted for full model |
|
C |
C adjusted for A, B. |
C adjusted for A, B |
C adjusted for full model |
7.3.1.4. ANOVA Interaction Selection
This dialogue does not appear if at least two [Factor] columns have been selected in the Variable Selection Dialogue.
The interaction terms to be included in the model are selected here. If higher order interactions are included, then all the related lower order interactions are automatically included. That is, if ABC is selected then AB, AC and BC are all included in the model automatically. Maximum three way interactions are possible.
